
Что такое молекулярно-кинетическая теория
Молекулярно-кинетическая теория (МКТ) -- раздел молекулярной физики, который стоится на изучении свойств вещества основываясь на их внутреннем молекулярном строении.
Основной постулат МКТ: вещество состоит из молекул, которые непрерывно хаотично движутся и взаимодействуют между собой по определенным законам. Движение молекул воспринимается как тепловое. Многие явления, происходящие в газах, жидкостях или твердых телах находят объяснения с точки зрения МКТ. Так, например, давление производимое газом на стенки сосуда объясняется как результат многочисленных соударений молекул газа на стенки сосуда. При этом молекулы передают стенкам свой импульс. Усредненная кинетическая энергия частиц определяет такой макропараметр как температура.
МКТ и статистическая физика
Молекулярно-кинетическая теория целиком опирается на статистические методы. Поэтому она часто именуется статистической физикой.
Статистической физикой называют раздел физики, в котором изучают макроскопические свойства систем, состоящих из очень большого числа частиц (молекул, атомов, электронов), через свойства этих частиц и взаимодействие между ними.
Статистическая физика рассматривает системы, находящиеся в равновесном состоянии (равновесная статистическая физика) и неравновесных состояниях физическая кинетика.
Как строится такая физика? В отличие от термодинамики она исходит не из общих принципов, а из модели молекулярного строения рассматриваемого объекта. Опираясь на механику (атомы рассматриваются как механические системы) и статистику она выводит затем те или иные термодинамические закономерности. Главное ее достоинство - большая глубина объяснений, наблюдаемых свойств и явлений. Чистая ("феноменологическая") термодинамика описывает внутренние свойства тел, не анализируя их строения. В чистой термодинамике, например, отсутствует понятие атома. Статистическая физика, наоборот, начинает изучение явлений с описания строения тел. Она, может быть, не занимается подробным описанием атомов, однако атомы, их движение, их взаимодействие являются основными понятиями статистической физики, на которых строится модель. Эта модель в той или иной мере упрощает, что ведет к ограниченности выводов, получаемых на ее основе.
Статистические закономерности
Поведение систем, состоящих из большого числа частиц, определяется статистическими закономерностями, которые существенно отличаются от законов механики. Поведение отдельных частиц, входящих в систему, например, траектория частицы, при статистическом описании системы оказывается несущественным. Поэтому изучение свойств системы сводится к отысканию средних значений физических величин, характеризующих состояние системы как целого. Существенное отличие систем, которые подчиняются статистическим законам, состоит в том, что поведение и свойства в значительной степени не зависят от их начального состояния.
Связь между динамическими закономерностями (описывающими движения отдельных частиц) и статистическим закономерностями проявляется в том, что свойства макроскопической системы определяется законами движения отдельных частиц.
В статистической физике используют эргодическую гипотезу. Согласно этой гипотезе предполагается, что в термодинамически равновесной системе средние по времени значения физических величин, характеризующие систему равны их средним статистическим значениям, то есть средним статистическим по равномерному распределению фазовых точек в тонком слое энергии, рассчитанным в один и тот же произвольный момент времени.
В классической статистической физике считается, что в термодинамически равновесной системе действует закон равномерного распределения энергии:
на каждую степень свободы частицы, образующих систему, в среднем, приходится одинаковая кинетическая энергия, равная:
\[E_k=\frac{i}{2}kT\left(1\right),\]где $i$- число степеней свободы молекулы, k- постоянная Больцмана, Т - термодинамическая температура.
При колебательном движении частица имеет как кинетическую, так и потенциальную энергию. Если колебания гармонические, то кинетическая и потенциальная энергии равны в среднем друг другу. Поэтому на одну колебательную степень свободы приходится в среднем энергия равная:
\[W=ikT\ \left(2\right).\]В качестве одного из примеров применения молекулярно-кинетической теории можно рассмотреть вывод выражения для давления газа.
Рассмотрим давление идеального газа в состоянии равновесия.
Давление определяется силой $\triangle F$, с которой газ давит на единицу площади $\triangle S$ стенки сосуда:
\[p=\frac{\triangle F}{\triangle S}(1.1)\]Сила есть импульс, передаваемый от тела к телу в секунду:
\[\triangle \overrightarrow{F}=\frac{\triangle \overrightarrow{p}}{\triangle t}(1.2)\]Значит, чтобы найти давление газа, нужно найти, какой импульс передаёт газ единице площади стенки сосуда в секунду. Займемся этим расчётом. Будем считать, что соударение отдельной молекулы со стенкой сосуда подчиняется законам упругого столкновения: молекула отскакивает от стенки с первоначальным по модулю импульсом и угол ее падения равен углу отражения (рис. 1).
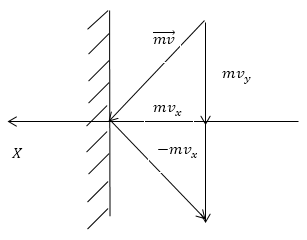
Рис. 1
В этом случае от молекулы стенке передаётся только х - составляющая импульса:
\[\triangle p_x=mv_x-\left(-mv_x\right)=2mv_x\ (1.3)\]Движение молекул в направлении других осей координат при передаче импульса выбранной стенке не существенно, и можно считать, что молекулы движутся только по оси х. (Движение по другим осям будет учтено в конце расчёта.) Найдем число столкновений молекул о площадку с единичной площадью стенки в секунду, если скорость молекулы равна $v_x$. Легко понять, что это число pавно числу молекул с данной скоростью, находящихся в цилиндре с основанием в единицу площади и высотой, численно равной $v_x$.(рис. 2) В самом деле, молекулы вне данного цилиндpа пpосто не попадут в течение секунды на заданную единицу площади стенки (или не долетят до стенки, или ударятся о стенку не в том месте).
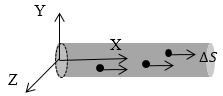
Рис. 2
Наоборот, все молекулы, попадающие в цилиндр, проходя за секунду путь, равный $v_x$, попадут на данную площадь стенки сосуда. Обозначим число молекул, обладающих заданной скоростью $v_x$ и находящихся в единице объема газа, через $n_{vx}$ Тогда число молекул, попадающих в цилиндp, или число молекул, удаpяющихся о стенку со скоpостью $v_x$ равно: $v_xn_{vx}$.
Эти молекулы передают стенке импульс, равный:
\[{2mv_xv_xn}_{vx}=2mv^2_xn_{vx}\left(1.4\right)\]Полный же импульс, который получает стенка на единице площади, т.е. давление газа, определяется суммированием таких выражений по всем возможным положительным значениям скорости молекулы:
\[p=\sum\limits_{v_x>0}{2mv^2_xn_{vx}(1.5)}\]Обозначим через n полное число молекул в единице объема газа. Половина из них летит к стенке (имеет скорость $v_x>0$). Перепишем формулу (1.5) в виде:
\[p=2m\frac{\sum\limits_{v_x>0}{v^2_xn_{vx}}}{\frac{n}{2}}\frac{n}{2}\ (1.6)\]и учтем, что выражение $\frac{\sum\limits_{v_x>0}{v^2_xn_{vx}}}{\frac{n}{2}}$представляет собой средний квадрат скорости молекулы. Средние величины будем обозначать скобками $$. Следовательно, формулу (1.6) можно переписать так:
\[p=2\frac{m }{2}n\ \left(1.7\right)\]Наконец, учтем, что скоpости молекул газа pаспpеделены по напpавлениям pавномеpно (газ изотpопен), и, следовательно,
\[ =++=3 (1.8)\]Поэтому окончательно формулу для давления газа представим в виде:
\[p=\frac{2}{3}\frac{m }{2}n= \frac{2}{3} n(1.9)\]Итак, давление идеального газа в состоянии равновесия равно двум третям произведения средней кинетической энергии поступательного движения молекулы газа на число молекул в единице объема газа.
Задание: Кислород находится в сосуде при T=300K. Определить среднюю энергию вращательного движения молекул.
Решение: Кислород имеет в молекуле 2 атома, следовательно у него 2 вращательные степени свободы, для вычисления энергии используем формулу (2.1) при i=2:
\[=\frac{i}{2}kT=kT(2.1)\]Проведем вычисления:
\[










