
Что такое давление
Давление (p) важный макроскопический параметр, который характеризует состояние системы. Если кроме давления для данной массы газа известна температура или объем, то состояние системы определено однозначно, т.е. все остальные параметры можно рассчитать, используя законы и уравнения МКТ.
Это физическая величина, которая определяется как:
где $F_n$ проекция силы на нормаль к поверхности S, на которую эта сила действует, S -- площадь тела.
Давление газа
Как уже неоднократно отмечалось, давление газа возникает в результате ударов молекул о стенки сосуда. Если мы считаем, что молекулы взаимодействуют со стенкой по законам абсолютно упругого удара, то частица передает стенке импульс, равный изменению импульса самой молекулы. Направим ось Х перпендикулярно стенке (рис.1), в этом случае изменение импульса стенки при ударе одной молекулой:
где $m_0$- масса молекулы.
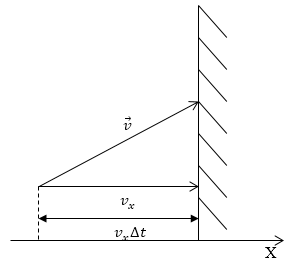
Рис. 1
Поток импульса, который передается стенке за счет ударов молекулами, которые движутся со скоростями близкими к v, направлен к стенке, равен $nf(v)m_0{v_x\ }^2dv$, отсюда:
где
В результате непосредственного интегрирования получаем:
Так как мы уже отмечали, что рассматриваем единичную площадку стены в течение времени. равном 1с, то можно записать, что давление будет равно:
Давление газа изотропно, это величина скалярная.
При постоянном объеме давление газа массы m подчиняется закону Шарля:
где $p_0$- давление газа при температуре $T_0=273\ К$.
Давление смеси идеальных газов равно сумме их парциальных давлений:
\[p=\sum\limits^N_{i=1}{p_i}\ \left(7\right).\]Уравнение (7) имеет название -- это закон Дальтона.
Парциальным давлением называют давление компоненты смеси газа, каким оно бы было, если бы других газов в смеси не было.
Ряд важных уравнений молекулярной физики, в которые входит давление:
- Уравнение состояния идеального газа(1): $p=nkT$(8).
- Уравнение состояния идеального газа(2) в виде уравнения Менделеева - Клайперона: $pV=\nu RT$(9).
- Основное уравнение МКТ: \[p=\frac{2}{3}n\left\langle E_k\right\rangle \left(10\right).\]
- Работа газа: \[dA=pdV\ \left(11\right).\]
Задание: В процессе сжатия 1-2 с линейной зависимостью р(V). Давление идеального газа возросло в 3 раза. Затем газ сжали в изобарном процессе 2-3 до первоначального объема. Найти отношение работ, совершенных газом в процессах расширения и сжатия. Температуры в состояниях 1 и 2 считать одинаковыми.
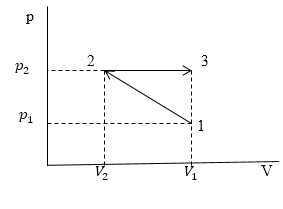
Рис. 2
Решение:
Работу газа (или над газом) можно рассчитать по формуле:
\[A=\int\nolimits^{V_2}_{V_1}{pdV}\ (1.1)\]Если мы рассматриваем процесс (как в условиях нашей задачи) в осях p(V), то исходя из геометрического смысла интеграла работа A будет равна площади криволинейной трапеции (в общем случае), а в нашем площади прямоугольника, когда газ расширяется и площади трапеции, когда газ сжимают. Найдем эти площади.
Площадь прямоугольника:
\[{{A_{2\to 3}=S}_{2\to 3}=(V}_1-V_2)(p_2)(1.2)\]Площадь трапеции:
\[{A_{1\to 2}=S}_{1\to 2}=(\frac{p_2+p_1}{2}){(V}_1-V_2)\ (1.3)\]Из условий задачи имеем:
\[p_2=3p_1\ \left(1.4\right)\]Найдем отношение $\frac{A_{2\to 3}}{A_{1\to 2}}$:
\[\frac{A_{2\to 3}}{A_{1\to 2}}=\frac{3p_1{(V}_1-V_2)}{\frac{4p_1}{2}{(V}_1-V_2)}=\frac{3}{2}\]Ответ: Работа, которую совершает газ в процессе 2-3 в 1,5 больше, чем работа по сжатию газа при заданных условиях.
Задание: Определите, как изменяется давление постоянной массы идеального газа, если в процессе объем увеличивают, температура уменьшается?
Решение:
За основу решения возьмем уравнение Менделеева -- Клайперона:
\[pV=\nu RT\left(2.1\right).\]Выразим из него давление:
\[p=\frac{\nu RT}{V}\to p\sim \frac{T\downarrow }{V\uparrow }\to p\downarrow \]Ответ: В данном процессе давление уменьшается.
Задание: В процессе, график которого приведен на рисунке (рис.3) давление $p\sim T^n.\ $Найти значение n, если масса газа постоянна.
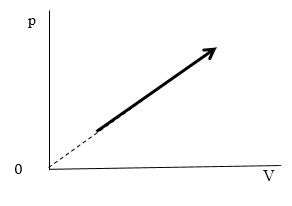
Рис. 3
Решение:
Из рисунка имеем зависимость p(V):
\[p\sim V\ \left(3.1\right)\]Из уравнения Менделеева -- Клайперона:
\[pV\sim \ T\left(3.2\right)\]Используем (3.1) заменив объем, получим:
\[p^2\sim T\ \left(3.3\right)\]Ответ: Получили $p\sim T^{\frac{1}{2}}$, следовательно, $n=\frac{1}{2}.$











