Плазма -- ионизированный квазинейтральный газ, который занимает настолько большой объем, что в нем не происходит заметного нарушения квазинейтральности вследствие тепловых флуктуаций. Квазинейтральность газа означает, что число положительных и отрицательных зарядов в нем почти одинаково.
Плазма возникает в положительном столбе тлеющего разряда. Она образуется в главном канале искрового разряда.
Так как концентрация электронов и положительных ионов в плазме одинаково, то объемный заряд равен нулю. По своей электропроводности ионная плазма приближена к металлам.
В том случае, если плазма находится в электрическом поле, то в ней появляется электрический ток и выделяется тепло. Причем, энергию в поле получают сначала электроны, затем электроны передают энергию ионам при соударениях. Но, надо заметить, что из-за большой разницы в массе, электрон передает не всю энергию иону. Если давление низкое, количество соударений мало, что приводит к тому, что средняя кинетическая энергия электронов больше средней кинетической энергии ионов. Это означает, что температура электронного газа в плазме выше температуры ионного газа (неизотермическая плазма, двух температурная плазма). В плазме возможно существование таких квазиравновесных состояний, которые в известном приближении могут характеризоваться двумя температурами.
При повышении давления увеличивается число соударений и улучшается теплообмен между электронным и ионным газами, при этом разность между их температурами уменьшается. При довольно высоком давлении плазма изотермическая.
В лабораторных условиях плазма может быть получена не только в газовых разрядах. Например, в электропроводящих твердых телах электронный газ и неподвижные положительные ионы решетки, так же образуют электронно-ионную плазму.
Основная масса вещества в космосе находится в виде сильно ионизированной плазмы. Так, к примеру, Солнце полностью состоит из плазмы. Верхние слои атмосферы Земли (ионосфера) является плазмой.
Плазма имеет сходство с обычными газами и подчиняется некоторым газовым законам. Однако между плазмой и обычными газами есть существенные отличия. Различия особенно проявляются в магнитном поле, когда на ионы и электроны действуют силы Лоренца, которых нет в газе, состоящем из нейтральных атомов. Ионы и электроны в плазме взаимодействуют при помощи кулоновских сил. Эти явления проявляются в свою очередь в уравнениях, которые описывают процессы, которые происходят в плазме.
Изучение свойств плазмы имеет практическое значение, так как с ее помощью появляется возможность управления термоядерными реакциями.
Электропроводность плазмы
Проведем оценку удельной проводимости ($\sigma $) полностью ионизированной плазмы, которая состоит из электронов и положительных ионов, имеющих заряд Z$q_e$ каждый. Так как массы ионов достаточно велики, то их движение в сравнении с движением электронов можно не учитывать (ток создается движением электронов). Величину $\sigma \ $ будем определять столкновениями электронов с ионами. Столкновения электронов между собой на силу тока не влияют, так как при их столкновениях суммарный импульс электронов не изменяется. Между электронами и ионами действуют кулоновские силы притяжения. Они являются дальнодействующими. Для того, чтобы движение электрона изменялось очень резко, он должен очень близко подойти к иону, что случается довольно редко. Существенно большее значение имеет в нашем случае взаимодействие электрона с большим числом ионов одновременно, при этом траектория движения иона изменяется плавно. Большие отклонения электрона от первоначального направления движения происходят в результате объединения малых отклонений. В данном случае о столкновениях, длине свободного пробега говорят в условном смысле. Так, временем свободного пробега в данном случае удобно называть промежуток времени ($\tau $), в течение которого направление движения электрона изменяется на угол $90^0$.
Оценим время свободного пробега электрона, в поле положительно заряженного иона (заряд иона Z$q_e$). Отклонение траектории электрона около иона составит угол ($\alpha $) равный:
где $m_e$ -- масса электрона, $v$ -- скорость электрона, $b$ -- прицельный параметр. При этом прицельный параметр, для которого $\alpha =90{}^\circ $, определён как:
Параметру $b$ формулы (2) соответствует «эффективное поперечное сечение» $s$,равное:
Если учитывать далекие взаимодействия, то результат, полученный в выражении (3) увеличивают в $L$ раз, где $L$- кулоновский логарифм, он практические не зависит от температуры и плотности плазмы. Так, например, для плазмы из полностью ионизованного дейтерия, при $kT\approx {10}^3эВ$ и концентрации электронов $n\approx {10}^{13}см^{-3}$ $L\approx 15.$ То есть получают:
Средняя длина свободного пробега $\left\langle \lambda \right\rangle \ $равна:
Время свободного пробега ($\tau $) равно:
Используем выражение: $m_ev^2\approx 3kT$, получим:
Из выражения (7) найдем удельную проводимость плазмы:
Приведенный способ получения выражения (8) следует считать оценкой удельной проводимости, а не доказательством. Из выражения (8) видно, что проводимость плазмы растет пропорционально абсолютной температуре в степени $\frac{3}{2}$ и в горячей плазме становится очень высокой. Еще быстрее с увеличением температуры растет теплопроводность плазмы, а именно пропорционально ${\left(kT\right)}^{\frac{5}{2}}$.
Соответственно, удельное сопротивление плазмы при высоких температурах очень не велико, так удельное сопротивление нержавеющей стали ${\rho }_{st}=7\cdot {10}^{-7}Ом\cdot м$, плазмы при $T=10^4эB$ ${\rho }_p=5\cdot 10^{-10}Ом\cdot м$.
Задание: Основной практический интерес в изучении плазмы состоит в решении проблемы управляемого термоядерного синтеза. Какова суть процесса и в чем состоит роль плазмы в данном процессе?
Решение:
Для активации интенсивных термоядерных реакций вещество необходимо нагреть до температуры в несколько десятков кило электрон вольт. При данных температурах любое вещество находится в состоянии плазмы. Самыми перспективными на сегодняшний день, «рабочими веществами» для термоядерного реактора считают изотопы водорода $(дейтерий (D)$ и $тритий (T))$. Термоядерную реакцию проще получить в смеси этих изотопов.
Термоядерные реакции должны происходить относительно плавно и медленно, поэтому появляется необходимость длительно удерживать горячую плазму в ограниченном объеме рабочего пространства, изолируя ее от стенок камеры. С этой целью используют магнитную термоизоляцию (то есть сильное магнитное поле). Это поле не дает возможности ионам и электронам перемещаться в поперечном направлении и попадать на стенки камеры.
Условие, которое должно удовлетворяться в термоядерном реакторе: энергия выделяемая в ходе реакций должна с избытком компенсировать затраты энергии, которые требуются для проведения данных реакций. Основные потери энергии при этом: тормозное излучение электронов при кулоновских столкновениях, магнитотормозное излучение, которое появляется при движении электронов в магнитном поле. Для того чтобы термоядерная реакция была самоподдерживающейся плазму необходимо нагреть до «критической» температуры. Она составляет 50 кэВ для чистого дейтерия и 10 кэВ для смеси в равных долях дейтерия и трития. При этом должен выполняться некоторое условие (критерий Лоусона), а именно:
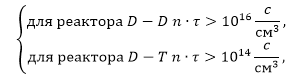
Рисунок 1. где n – концентрация ионов плазмы одного знака, τ – среднее время удержания плазмы
Основная проблема при создании реакции управляемого термоядерного синтеза в получении устойчивой плазмы. Так как из-за дальнодействующего характера кулоновских сил в плазме происходит множество коллективных процессов, возникают шумы и колебания, которые вызывают неустойчивость плазмы. Так, основной задачей становится подавление этих неустойчивостей.
Задание: Как изменится удельное сопротивление дейтериевой плазмы при температуре T, если плотность ее увеличить в 3 раза?
Решение:
В качестве основы для решения задачи используем формулу, для оценки проводимости плазмы в виде:
\[\sigma =\frac{{\left(3kT\right)}^{\frac{3}{2}}}{\pi {{ZLq}_e}^2\sqrt{m_e}}\left(2.1\right).\]Удельное сопротивление ($\rho $) -- величина обратная проводимости, то есть:
\[\rho =\frac{1}{\sigma }\approx \frac{\pi {{ZLq}_e}^2\sqrt{m_e}}{{\left(3kT\right)}^{\frac{3}{2}}}\left(2.2\right).\]Из выражения (2.2) видно, что удельное сопротивление плазмы не зависит от ее плотности, зависит только от температуры.
Ответ: Не изменится.











