Длина волны - минимальное расстояние между двумя точками одной и той же фазы колебаний.
Длина волны обычно обозначается греческой буквой лямбда $\left(\lambda \right)$.
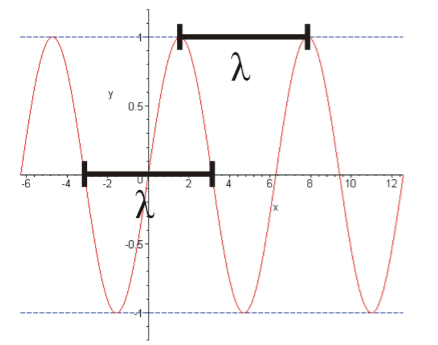
Рисунок 1. Определение длины волны
Длина волны зависит от среды, через которую она проходит (например, вакуум, воздух или вода).
Примерами волнообразных явлений могут служить звуковые волны, свет или ветровые волны.
Синусоидальные волны
В линейных средах, любая волновая картина может быть описана независимо от распространения синусоидальных компонентов. Длина волны $\lambda $ синусоидального сигнала движения при постоянной скорости $v$ задается:
где $v-$ фазовая скорость волны.
В диспергирующей среде, сама фазовая скорость зависит от частоты волны.
В случае электромагнитного излучения, фазовая скорость является скоростью света, которая приблизительно равна ${\rm 3\cdot}{{\rm 10}}^{{\rm 8\ }}{{\rm м}}/{{\rm с}}$. Для звуковых волн в воздухе, скорость звука составляет ${\rm 343}{{\rm м}}/{{\rm с}}{\rm \ \ }$(при комнатной температуре и атмосферном давлении).
Стоячие волны
Стоячие волны - это волны в среде, в которой каждая точка на оси волны имеет связанную с ней постоянную амплитуду.
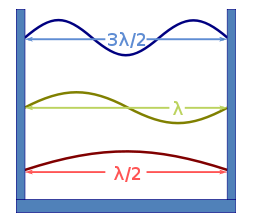
Рисунок 2. Синусоидальные стоячие волны
Стационарные волны можно рассматривать как сумму двух бегущих синусоидальных волн с противоположно направленными скоростями. Следовательно, длина волны, период, и скорость волны связаны так же, как и для бегущей волны. Например, скорость света может быть определена из наблюдения стоячих волн в металлическом корпусе, внутри которого находится идеальный вакуум.
Математическое представление
Синусоидальные волны часто представляются математически:
где $y$ есть значение волны в любом положении $x$ и времени $t$, ${\rm A}$ является амплитудой волны.
Или, используя волновые числа и угловую частоту:
Где длина волны и волновое число связаны со скоростью и частотой, как:
или
Для электромагнитных волн скорость в среде определяется ее показателем преломления в соответствии:
Чему равна длина волны, которая распространяется со скоростью $5$ м/с и в которой за $10$ с успевают произойти $4$ колебания?
Решение:
\[\lambda =v\cdot T\]Где период
\[T=\frac{t}{n}=\frac{10\ c}{4}=2,5\ c\] \[\lambda =5\frac{м}{с}\cdot 2,5\ с=12,5\ м\]Ответ: $\lambda =12,5\ м$
Найти длину волны $\lambda $ колебаний, если расстояние между первой и четвертой стоячей волны $l=15\ см.$
Решение:
Длина стоячей волны
\[{\lambda }_{ст}=\frac{\lambda }{2}\ (1)\]где $\lambda -$ длина волны колебаний.
С другой стороны
\[{\lambda }_{ст}=\frac{l}{n_1-n_2}\ (2)\]Где $n_1и\ n_2-$ порядковые номера пучностей.
По условию
$n_1=1$ и $n_2=4$
Тогда приравнивая правые части уравнений (1) и (2), получаем
\[\frac{\lambda }{2}=\frac{l}{3}\]Откуда длина волны колебаний
\[\lambda =\frac{2l}{3}=10\ см=0,1\ м\]Ответ:$\ \lambda =0,1\ м$.












