Определение молекулярного тока
Магнитное поле, подобно полю электрическому может быть макроскопическим и микроскопическим. Микроскопическое поле возникает в результате движения элементарных зарядов в веществе. Макроскопическое поле -- результат усреднения микроскопических полей по бесконечно малым объемам пространства. Вращения электронов и ядер атомов по отношению к создаваемому ими магнитному полю эквивалентны токам, которые текут в атомах вещества. Средняя плотность такого тока в веществе равна нулю, переноса электрического заряда на макроскопические расстояния не происходит.
Итак, токи эквивалентные тем, которые возникают при движении элементарных зарядов в молекулах и атомах вещества, называют молекулярными токами.
В ненамагниченных магнетиках молекулярные токи распределены хаотично, их магнитные поля в среднем взаимно компенсируют друг друга. Намагниченный магнетик можно характеризовать упорядоченным характером молекулярных токов, благодаря чему результирующее магнитное поле вещества не равно нулю.
В тех магнетиках, которые являются проводниками (например, металлы) различают токи проводимости (плотность тока проводимости $\overrightarrow{j_{pr}}$), которые относят к упорядоченному движению заряда в макроскопическом понимании (например, движению свободных электронов в металле) и молекулярные токи ($\overrightarrow{j_m}$), тогда микроскопическую плотность тока ($\overrightarrow{j_{mik}}$) в среде вычисляют как:
\[\overrightarrow{j_{mik}}=\overrightarrow{j_m}+\overrightarrow{j_{pr}}\ \left(1\right).\]Часто предполагают, что отличие токов проводимости от молекулярных токов в том, что молекулярные токи замыкаются внутри микроскопически малых объектов пространства. Подобное разделение токов на два типа упрощает вывод макро уравнений поля из посылок электронной теории.
Молекулярные токи и индукция магнитного поля
Для того, чтобы вычислить индукцию макроскопического поля молекулярные токи заменяют макроскопическими токами, которые непрерывно изменяются в пространстве. Такие токи имеют название токов намагничивания. Дальше эти плотность этих токов будем обозначать $\overrightarrow{j_m}$. Плотность токов проводимости будем обозначать $\overrightarrow{j}$. Так получаем, что магнитное поле порождается токами проводимости и токами намагничивания. Если известны эти токи, то можно вычислять индукцию поля $\overrightarrow{B},$ используя формулы для вакуума. В таком случае теорема о циркуляции вектора индукции магнитного поля будет иметь вид:
\[\oint\limits_L{\overrightarrow{B}\overrightarrow{dl}}={\mu }_0\left(I+I_m\right)\left(2\right)\]или в дифференциальной форме:
\[rot\overrightarrow{B}={\mu }_0\left(\overrightarrow{j}+{\overrightarrow{j}}_m\right)\left(3\right),\]где I -- ток проводимости, $I_m$ -- ток намагничивания, полные токи, которые пронизывают контур L.
Итак, возникновение магнитных моментов связано с наличием круговых токов. Токи в элементарных объемах, которые приводят к возникновению магнитных моментов, назвали молекулярными токами. Однако не следует воспринимать этот термин буквально. Молекулярные токи, строго говоря, могут течь только внутри молекулы. При определении намагниченности и других параметров имеют в виду усредненные величины. Магнитные моменты представляют размазанными по объему вещества, а молекулярные токи текущими по всему объему.
Намагниченность
Для характеристики состояния намагниченного состояния магнетика используют вектор намагниченности $(\overrightarrow{J})$.
Намагниченностью ($\overrightarrow{J}$) называют физическую величину, которая равна:
\[\overrightarrow{J}=\frac{1}{\triangle V}\sum\limits_{\triangle V}{{\overrightarrow{p}}_{mi}(4)},\]где $\triangle V$ -- элементарный объем, $\overrightarrow{p_{mi}}$ -- магнитные моменты молекул, суммирование осуществляется по всем молекулам в объеме $\triangle V$. Из формулы (4) имеем, что:
\[p_m=\overrightarrow{J}dV\left(5\right).\]Связь намагниченности с молекулярными токами
Рассмотрим бесконечно маленький замкнутый контур L, который ограничивает элемент площади $\triangle S$ (рис.1). Вычислим циркуляцию намагниченности ($\overrightarrow{J}$) по контуру:
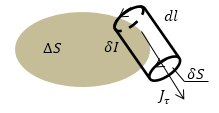
Рис. 1
\[\int\limits_L{\overrightarrow{J}\overrightarrow{dl}=\int\limits_L{J_{\tau }dl}\left(6\right),}\]где $J_{\tau }$- тангенциальная составляющая вектора намагниченности вдоль контура L. Эта составляющая возникает за счет токов, которые текут по замкнутым контурам вокруг линии, вдоль которой проводится интегрирование. Умножим и разделим правую часть выражения (6) на величину $\delta S$ (площадь которую обтекает ток в плоскости, которая перпендикулярная линии интегрирования), проведем преобразования в том числе используя выражение (5):
\[\int\limits_L{J_{\tau }dl}=\int\limits_L{J_ф\frac{dl\delta S}{\delta S}}=\int\limits_L{J_{\tau }\frac{dV}{\delta S}}=\int\limits_L{\frac{dp_m}{\delta S}}\left(7\right).\]В соответствии с определением магнитного момента ($p_m=IS\to {dp}_m=\delta I\delta S,\ $)$\ где\ \delta I\ сила\ тока,\ который\ обтекает\ площадку\ \ \delta S,$ причем$\ \delta I$ пересекает $\triangle S$ по нармали. Получаем из (7):
\[\int\limits_L{\frac{dp_m}{\delta S}}=\int\limits_L{\frac{\delta I \delta S}{дS}}=\int\limits_L{\delta I}=\triangle I_n\left(8\right),\]где $\triangle I_n$- нормальная составляющая силы тока, которая пересекает площадку $\triangle S.$ В результате мы получили:
\[\int\limits_L{\overrightarrow{J}\overrightarrow{dl}=\triangle I_n\left(9\right).}\]Из выражения (9) легко получить:
\[\overrightarrow{j_m}=rot\overrightarrow{J}\left(10\right).\]Формула (10) -- выражение для объемной плотности молекулярных токов, которые являются причиной намагниченности $\overrightarrow{J}$.
Молекулярные токи могут течь и по поверхности раздела меду магнетиками или между магнетиком и вакуумом. Тогда поверхностная плотность молекулярного тока ($i_{m.p}=\frac{\triangle I_{m.pov}}{l}$) равна:
\[\overrightarrow{i_{m.p}}=\overrightarrow{n}\times \left(\overrightarrow{J_2}-\overrightarrow{J_1}\right)\left(11\right),\]где $\overrightarrow{n}$ -- единичные вектор нормали к поверхности раздела, направленные во вторую среду.
Задание: Получите формулу, связывающую объемную плотность молекулярных токов и вектор намагниченности ($\overrightarrow{j_m}=rot\overrightarrow{J}$).
Решение:
Найдем составляющую ротора вектора намагниченности в направлении нормали к площадке $\triangle S\ (рис.1)$. Используем определение ротора и равенство (1.1):
\[\int\limits_L{\overrightarrow{J}\overrightarrow{dl}=\triangle I_n\left(1.1\right).}\]получим:
\[{rot}_n\overrightarrow{J}={\mathop{lim}_{\triangle S\to 0} \frac{\int\limits_L{\overrightarrow{J}\overrightarrow{dl}}}{\triangle S}\ }={\mathop{lim}_{\triangle S\to 0} \frac{\triangle I_n}{\triangle S}=j_{mn}\ }\left(1.2\right),\]где ${\mathop{lim}_{\triangle S\to 0} \frac{\triangle I_n}{\triangle S}=j_{mn}\ }$
$j_{mn}$-- нормальная составляющая плотности молекулярных токов. Это логично, так как именно они отвечают за возникновение намагниченности.
Равенство (1.2) выполняется при любой ориентации площадки $\triangle S,$ то есть для любых компонент $rot\overrightarrow{J}\ $и $\overrightarrow{j_m}$. Следовательно, имеет место равенство:
\[\overrightarrow{j_m}=rot\overrightarrow{J}\left(1.3\right).\]Задание: Покажите, что поля постоянного магнита в виде цилиндра и поле соленоида с током эквивалентны.
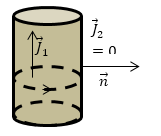
Рис. 2
Решение:
Найдем поверхностную плотность молекулярного тока однородного намагниченного цилиндра (рис.2), который является постоянным магнитом.
Намагниченность цилиндра ($\overrightarrow{J_1}$) изображена на рис.2 стрелкой. В вакууме намагниченность равна нулю $J_2=0.$ Нормаль $\overrightarrow{n}$ -- внешняя нормаль к цилиндру. В соответствии с формулой:
\[\overrightarrow{i_{m.p}}=\overrightarrow{n}\times \left(\overrightarrow{J_2}-\overrightarrow{J_1}\right)\left(2.1\right),\]плотность поверхностного молекулярного тока, который течет по цилиндру, равна:
\[\overrightarrow{i_{m.p}}=\overrightarrow{n}\times \left(-\overrightarrow{J_1}\right)=\overrightarrow{J_1}\times \overrightarrow{n}\left(2.2\right).\]Одна из линий тока показана как окружность со стрелкой. Намагниченность $\overrightarrow{J_1}$ составляет с текущим по поверхности током правовинтовую систему. Из формулы:
\[rot\overrightarrow{J_1}=0\ \left(2.3\right).\]следует, что объемные молекулярные токи внутри цилиндра отсутствуют.
Ответ: Поле вне цилиндра создано поверхностными молекулярными токами, которые текут по окружностям. Этим доказано, что поля постоянного цилиндрического магнита и поле соленоида эквивалентны.












