Причины использования материального уравнения
Фундаментальным уравнением магнитостатики в дифференциальной форме, является выражение:
где $\overrightarrow{j}$ -- плотность тока. Уравнение (1) является полевым и применяется для описания магнитостатического поля. Однако, при рассмотрении конкретных примеров этого уравнения не достаточно, так ка уравнение (1) не содержит ни каких постоянных, которые характеризовали бы свойства среды, в которой возбуждается поле. Для того чтобы при описании поля учесть свойства вещества вводят уравнение, которое называют материальным уравнением для векторов магнитного поля.
Принципиальный способ получения материальных уравнений дают молекулярные теории поляризации, намагничивания и электрической проводимости среды. В основе этих теорий положены идеализированные модели вещества. К таким моделям применяют уравнения классической или квантовой механики методы статистической физики и находят связь между векторами магнитной индукции и напряжённостью магнитного поля. Получают более или менее сложные соотношения, которые и дополняют фундаментальные уравнения.
Материальное уравнение для векторов магнитного поля в простейшем случае
Самое простое материальное уравнение для векторов магнитного поля получено для слабых полей, которые медленно изменяются во времени и пространстве. В таком случае для изотропных неферромагнитных сред материальное уравнение имеет вид:
где ${\mu }_0$ -- магнитная постоянная$,\mu $ -- магнитная проницаемость среды, характеризующая магнитные свойства среды.
Учет магнитных свойств, феноменологически описываемых намагниченностью, содержится в магнитной проницаемости ($\mu $). Когда Максвелл в свою теорию вводил материальное уравнение вида (2), он рассматривал магнитную проницаемость среды как постоянную величину, введенную в теорию из опыта. Электронная теория показала, что материальное уравнение в виде (2) выполняется, если соблюдаются условия:
- за время приблизительно равное собственному периоду внутриатомных колебаний поле должно изменяться мало;
- поле должно изменяться на очень небольшую величину на расстояниях сравнимых с размерами атомов и молекул.
Итак, обычно считают, что материальное уравнение (2) выполняется, если $\mu $ может зависеть от координат, но не зависит от времени и векторов поля. В поле отсутствуют магниты и ферромагнитные тела.
Для учета движения среды сводят к движению зарядов или токов в среде. Тогда уравнение (1) не изменяется, а материальное уравнение (2) становится зависимым от скорости движения среды и что существенно их усложнит.
Надо отметить, что уравнение (2), как и остальные материальные уравнения электромагнитного поля хоть и является весьма значимым в теории, но фундаментальным не является и общностью, такой как уравнение (1) не обладает.
Задание: Определите индукцию магнитного поля (B) и намагниченность (J) сердечника тороида, который имеет N=151 виток. Средний радиус тороида R=3 см. Сила тока в тороиде I=1 А. Используйте график зависимости В(H) рис.1.
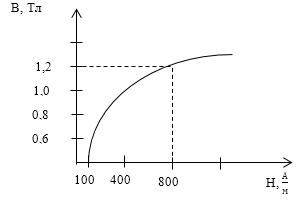
Рис. 1
Решение:
За основу решения задачи примем формулу, определяющую напряженность магнитного поля в тороиде:
\[H=In\ \left(1.1\right),\]где $n$ -- число витков тороида на единицу длины. Найдем эту величину как:
\[n=\frac{N}{l}=\frac{N}{2\pi R}\left(1.2\right).\]Тогда выражение (1.1) примет вид:
\[H=I\frac{N}{2\pi R}\ \left(1.3\right).\]Для того, чтобы далее воспользоваться графиком (рис.1) проведем вычисление напряженности поля:
\[H=1\frac{151}{2\cdot 3,14\cdot 3\cdot {10}^{-2}}\approx 800\ \left(\frac{А}{м}\right).\]Используя график получим, что при $H=800\frac{А}{м}$ индукция магнитного поля В=1,2Тл.
Зная материальное уравнение для векторов магнитного поля, в применении к нашему случаю запишем его, как:
\[B=\mu {\mu }_0H\left(1.4\right),\]из уравнения (1.4) выразим магнитную проницаемость вещества:
\[\mu =\frac{B}{{\mu }_0H}\left(1.5\right).\]Намагниченность связана с напряжением магнитного поля формулой:
\[J=\varkappa H=\left(\mu -1\right)H\left(1.6\right),\]где $\varkappa $ магнитная восприимчивость. Используя (1.5), получим, что:
\[J=\left(\mu -1\right)H.\]Вычислим магнитную проницаемость вещества:
\[\mu =\frac{1,2}{4\cdot \pi \cdot 800}\approx 1,19\cdot {10}^3\]Проведем вычисление намагниченности:
\[J=(1,19\cdot {10}^3-1)\cdot 800\approx 952\cdot 10^3(\frac{А}{м}).\]Ответ: В=1,2Тл, $J=952\cdot 10^3\frac{А}{м}.$
Задание: Бесконечно длины соленоид находится в диамагнитной среде, длина соленоида равна l, площадь поперечного сечения S, число витков N. Индуктивность соленоида L, сила тока в нем I. Найдите намагниченность внутри соленоида и его магнитную индукцию.
Решение:
Зная материальное уравнение, которое связывает напряжённость магнитного поля и индукцию для нашего соленоида:
\[B=\mu {\mu }_0H\ (2.1)\]напряжённость поля длинного соленоида:
\[H=\frac{N}{l}I\ (2.2)\]и формулу для индуктивности соленоида:
\[L={\mu }_0\mu \frac{N^2}{l}S\ (2.3)\]найдем индукцию магнитного поля соленоида. Для этого выразим из (2.3) магнитную проницаемость среды, подставим ее в уравнение (2.1), так же подставим в (2.1) напряженность из (2.2), получим:
\[B={\mu }_0\frac{Ll}{N^2S{\mu }_0}\frac{N}{l}I=\frac{L}{NS{\mu }_0}I\left(2.4\right).\]Вектор намагниченности связан с вектором напряженности, в нашем случае можно записать, что:
\[J=\left(\mu -1\right)H=\left(\frac{Ll}{N^2S{\mu }_0}-1\right)\frac{N}{l}I.\]Ответ: $B=\frac{L}{NS{\mu }_0}I,\ J=\left(\frac{Ll}{N^2S{\mu }_0}-1\right)\frac{N}{l}I.$











