Поведение магнитного поля в однородных магнетиках и полости магнетика
Следствием закона преломления линий поля при переходе границы раздела двух диэлектриков:
где ${\alpha }_1$ -- угол между линиями магнитной индукции в среде 1 и нормалью к поверхности раздела, ${\alpha }_2$- гол в среде 2 является то, что линии индукции, попадая в среду с большей магнитной проницаемостью, удаляются от нормали и сгущаются.
Вычисление распределения линий магнитной индукции весьма сложная задача, даже если иметь дело с телами простой формы. Допустим, что мы внесли в магнитное поле, которое было однородным, кусок магнетика, магнитная проницаемость которого больше, чем у окружающей среды. Внесённый в поле объект намагничивается и сам становится источником поля. Линии индукции стягиваются к магнетику, преломляются на его поверхности и располагаются внутри объекта гуще, чем вне его.
Если в однородное магнитное поле поместить полое тело, например цилиндр, стенки которого сделаны из вещества с магнитной проницаемостью больше, чем у окружающей среды, то линии магнитной индукции будут сгущаться в теле цилиндрической поверхности. В полости при этом густота линий уменьшится, это значит, что магнитное поле может быть ослаблено практически до нуля. Это происходит в результате сложения внешнего магнитного поля с полем намагнитившегося магнетика.
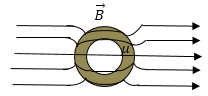
Рис. 1
Это явление используется для создания магнитной защиты или магнитной экранировки, то есть защиты приборов от воздействия внешнего магнитного поля. Оболочка из магнетика с большим $\mu $ работает как экран, который не допускает проникновения магнитного поля в пространство, которое ограничено оболочкой.
Сравнение явления экранировки магнитного поля с электростатической защитой
Внешне явление, ослабление магнитного поля в полости магнетика напоминает явление, которое лежит в основе электростатической защиты при помощи проводящей оболочки. Но, между этими явлениями существует принципиальное различие. У проводящей оболочки в электрическом поле стенки могут быть сколько угодно тонкими для того, чтобы можно было реализовать электростатическую защиту. Достаточно, например, посеребрить поверхность стеклянного сосуда, чтобы внутри такого сосуда, помещенного в электрическое поле, напряженность поля оказалась равной нулю. Электрическое поле обрывается на поверхности металла. Для магнитного поля тонкие стенки не являются защитой внутреннего пространства. Только толстые стенки магнетика могут ослабить поле на столько сильно, чтобы магнитная защита имела практическое значение, но и в таком случае поле внутри полости не будет равно нулю. При этом ослабление поля не является результатом обрыва силовых линий на поверхности магнетика. Линии магнитного поля не обрываются и, как обычно, являются замкнутыми, или уходят в бесконечность, проходя через магнетик. Ослабление магнитного поля внутри полости является следствием изменения направлений линий поля, а не их обрыва.
Задание: Шар из магнетика с магнитной проницаемостью ${\mu }_1$ радиусом R помещен в однородное магнитное поле с напряженностью $H_0$, которое создано в бесконечной среде с магнитной проницаемостью ${\mu }_2$. Считать, что токи проводимости отсутствуют. Найдите поле внутри шара. Исходя из полученной формулы, объясните, почему возможна магнитная экранировка.
Решение:
Магнитное поле, в котором отсутствуют токи проводимости, является потенциальным, то есть выполняется равенство:
\[rot\ \overrightarrow{H}=0\ \left(1.1\right).\]Токи проводимости отсутствуют как внутри шара, так и вне его, следовательно, поле потенциально во всем пространстве. Обозначим ${\varphi }_m$- потенциал этого поля. Тогда:
\[\overrightarrow{H}=-grad \varphi_m\left(1.2\right).\]Если среда однородна ($\mu =const$) уравнения $div\overrightarrow{B}=0$ и $div\overrightarrow{H}=0$ эквивалентны. Подставим (1.2) в (1.1), для всех точек вне шара (${\mu }_2=const$) и для всех точек внутри шара (${\mu }_1$) получим:
\[{{\nabla }^2\varphi }_m=0\ \left(1.3\right).\]Мы получили, что потенциал магнитного поля удовлетворяет уравнению Лапласа.
Поместим начало координат в центр шара, направим координатную ось сферической системы координат в направлении вектора $\overrightarrow{H_0.}$ В результате аксиальной симметрии уравнение Лапласа можно записать в сферической системе координат как:
\[\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial {\varphi }_m}{\partial r}\right)+\frac{1}{r^2sin\theta }\frac{\partial }{\partial \theta }\left(sin\theta \frac{\partial {\varphi }_m}{\partial \theta }\right)=0\ (1.4)\]К уравнению (1.3) добавим граничные условия:
\[B_{1n}=B_{2n}\ и\] \[H_{2\tau }-H_{1\tau }=j_{p\ \ }\left(1.5\right),\]где $j_{p\ \ }=0$ -- поверхностные токи проводимости. В математике известно общее решение такого уравнения. При желании подстановкой можно проверить, что функции ${\varphi }_{1m},\ {\varphi }_{2m}$ являются решениями уравнения Лапласа (1.4):
\[{\varphi }_{1m}=A_1rcos\theta +A_2r^{-2}cos\theta ,\ {\varphi }_{2m}={-H}_0rcos\theta +B_2r^{-2}cos\theta \left(1.6\right),\]где $A_1$, $A_2$,$\ B_2$ -- постоянные, которые удовлетворяют уравнению (1.4), $H_0$ -- модуль напряжённости магнитного поля на бесконечности.$\ {\varphi }_{1m}$ -- магнитный потенциал внутренней области шара, ${\varphi }_{2m}$ -- магнитный потенциал внешней области шара. Из (1.6) очевидно, что при $r\to 0,\ {\varphi}_{1m}\to \infty $. Значит $A_2=0.$ Потенциал должен быть непрерывен и это условие на границе имеет вид:
\[A_1Rcos\theta ={-H}_0Rcos\theta +B_2R^{-2}cos\theta (1.7)\]Из (1.7) получим:
\[A_1=B_2R^{-2}{-H}_0\left(1.8\right).\]Тангенциальная компонента ($H_{\tau }$) вектора $\overrightarrow{H}$ на поверхности шара равна:
\[H_{\tau }=H_{\theta }=-{\left\{\frac{1}{r}\frac{\partial {\varphi }_m}{\partial \theta }\right\}}_{r=R}(1.9)\]Условие $H_{1\theta }=H_{2\theta }$ выполняется, если выполняется (1.8). Нормальные составляющие вектора напряженности равны:
\[H_{1n}=H_{1r}=-{\left(\frac{\partial {\varphi }_{1m}}{\partial r}\right)}_{r=R}=-A_1cos\theta \ (1.10)\] \[H_{2n}=H_{2r}=-{\left(\frac{\partial {\varphi }_{2m}}{\partial r}\right)}_{r=R}=H_0cos\theta +2B_2R^{-3}cos\theta \left(1.11\right)\]Из условия:
\[{\mu }_1H_{1r}={\mu }_2H_{2r}\left(1.12\right)\]получим, что
\[A_1=-\frac{{\mu }_2}{{\mu }_1}\left({2B}_2R^{-3}{+H}_0\right)\left(1.13\right).\]Решая систему уравнений (1.8) и (1.13), получим:
\[A_1=-\frac{3{\mu }_2}{{\mu }_1+2{\mu }_2}H_0,B_2=\frac{{\mu }_1-{\mu }_2}{{\mu }_1+2{\mu }_2}R^3H_0\ \left(1.14\right).\]Тогда потенциалы на границе шара равны:
\[{\varphi }_{1m}=-\frac{3{\mu }_2}{{\mu }_1+2{\mu }_2}H_0rcos\theta \left(1.15\right).\] \[{\varphi }_{2m}={-H}_0rcos\theta +\frac{{\mu }_1-{\mu }_2}{{\mu }_1+2{\mu }_2}R^3H_0r^{-2}cos\theta ={-H}_0rcos\theta \left(1-\frac{{\mu }_1-{\mu }_2}{{\mu }_1+2{\mu }_2}R^3H_0r^{-3}\right)\left(1.16\right).\]Получаем, что внутри шара напряжённость магнитного поля постоянна и параллельна оси Z:
\[H_{1Z}=-\frac{\partial \varphi }{\partial z}=-\frac{\partial {\varphi }_{1m}}{\partial \left(rcos\theta \right)}=\frac{3{\mu }_2}{{\mu }_1+2{\mu }_2}H_0\left(1.17\right).\]$H_{1Z}$- напряженность магнитного поля, которое составлено из внешнего поля ($H_0$) и поля, которое создается в результате намагничивания. Поле, которое создается внутри шара, называют размагничивающим полем $(H_{razm})$. Название условно. Тогда:
\[H_{razm}=H_{1Z}-H_0=\frac{м_2-м_1}{м_1+2м_2}H_0\left(1.18\right).\]Очевидно, что при ${\mu }_2
Ответ: $H_{razm}=\frac{{\mu }_2-{\mu }_1}{{\mu }_1+2{\mu }_2}H_0.$
Задание: Используя результаты Примера 1. запишите выражение для вектора $H_{razm}$, при тех же условиях, что в примере 1, используя понятие вектора намагниченности. Чему будет равна напряженность поля в шаре (${H'}_{razm}$), если он находится в вакууме, а намагниченность шара равна $J_1$?
Решение:
На основании формул:
\[\overrightarrow{J}=\varkappa \overrightarrow{H}\left(2.1\right)\ и\] \[\mu =\varkappa +1\ \left(2.2\right).\]Получим:
\[J_1=\left({\mu }_1-1\right)H_{1z},J_2=\left({\mu }_2-1\right)H_0\left(2.3\right).\]Найдем разность:
\[J_2-J_1=\left({\mu }_2-1\right)H_0-\left({\mu }_1-1\right)\frac{3}{{\mu }_1+2{\mu }_2}H_0=\frac{\left(2{\mu }_2+1\right)\left({\mu }_2-{\mu }_1\right)}{{\mu }_1+2{\mu }_2}H_0\left(2.4\right).\]Следовательно, поле внутри шара может быть представлено как:
\[H_{razm}=\frac{{\mu }_2-{\mu }_1}{{\mu }_1+2{\mu }_2}H_0=\frac{J_2-J_1}{2{\mu }_2+1}\left(2.5\right).\]Если шар находится в вакууме, то ${\mu }_2=1\ и\ J_2=0$, получим, что:
\[{H'}_{razm}=-\frac{J_1}{3}.\]Ответ: $H_{razm}=\frac{J_2-J_1}{2{\mu }_2+1}.$ ${H'}_{razm}=-\frac{J_1}{3}.$












