Определение
Вещества, которые при внесении их в магнитное поле претерпевают такие изменения, что сами становятся источниками магнитного поля, называют магнетиками.
В этом процессе полная индукция магнитного поля равна сумме индукций внешнего магнитного поля и магнитного поля, которое рождено самим магнетиком. Процесс изменения состояния магнетика во внешнем магнитном поле называют намагничиванием. Магнитики были открыты Фарадеем в 1845 г.
Механизм намагничивания. Виды магнетиков
В зависимости от механизма намагничивания магнетики делят на диа-, пара- ферро- и ферримагнетики. Антиферромагнетики относят тоже к магнетикам, несмотря на то, что они не создают магнитного поля в пространстве.
Интенсивность намагничивания характеризуется тем, что все элементы объема вещества приобретают магнитный момент.
Диамагнетиками называют вещества, в которых при внесении во внешнее магнитное поле в молекулах и атомах изменяется движение электронов так, что образуется ориентированный круговой ток.
Этот ток характеризуют магнитным моментом ($p_m$):
\[p_m=IS\ \left(1\right),\]где $S$ -- площадь витка с током.
Говорят, что молекулы такого вещества в магнитном поле обретают индуцированный магнитный момент. Такие молекулы становятся источниками дополнительного поля, индукция такого поля определена как:
\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\left\{\frac{3(\overrightarrow{p_m}\cdot \overrightarrow{r})\overrightarrow{r}}{r^5}-\frac{\overrightarrow{p_m}}{r^3}\right\}\left(2\right).\]Диамагнетики намагничиваются во внешнем поле в направлении противоположном внешнему полю. Магнитная восприимчивость диамагнетика меньше нуля. Причем она много меньше единицы.
Диамагнетики делятся на «классические», «аномальные» и сверхпроводники. Классические диамагнетики имеют магнитную восприимчивость $\varkappa
Парамагнетиками называют вещества, в которых движение электронов в молекулах происходит так, что молекулы имеют постоянный магнитный момент и без магнитного поля. Молекула парамагнетика сама источник магнитного поля. В отсутствии магнитного поля магнитные моменты разных молекул ориентированы хаотично, результирующая индукция поля равна нулю, в результате тело не намагничено. Во внешнем магнитном поле постоянные магнитные моменты молекул ориентируются по внешнему полю, образуется преимущественное направление ориентации магнитных моментов. Малые объемы вещества получают магнитные моменты, которые равны сумме магнитных моментов отдельных молекул. Парамагнетик сам становится источником поля, он намагничивается в направлении внешнего поля. Магнитная восприимчивость ($\varkappa $) парамагнетика больше нуля, но, как и у диамагнетика весьма мала.
Парамагнетики делят на нормальные парамагнетики, парамагнитные металлы, антиферромагнетики. К группе нормальных парамагнетиков относят газы (кислород, оксид азота, платина, палладий и др.). Для этих парамагнетиков $\varkappa >0$ и она зависит от температуры по закону Кюри:
\[\varkappa =\frac{C}{T}\ (3)\]или закону Кюри -- Вейсса:
\[\varkappa =\frac{C'}{T+\triangle }\ \left(4\right),\]где C и C' -- постоянные Кюри, $\triangle $ - постоянная, которая бывает больше и меньше нуля.
У парамагнитных металлов магнитная восприимчивость не зависит от температуры. Эти металлы слабомагнитны $\varkappa \approx {10}^{-6}.$
Антиферромагнетики при температуре выше некоторой температуры, которую называют точкой Кюри становятся нормальными парамагнетиками.
Намагничивание ферромагнетиков и ферримагнетиков связывают с тем, что электроны имеют магнитный момент, который имеет определенное соотношение с механическим моментом - спином. В магнитном поле спины этих магнетиков определенным образом ориентируются. Это, как правило, кристаллические вещества. При невысокой температуре ферромагнетики обладают спонтанной намагниченностью. Она сильно изменяется под действием внешнего поля, при деформации ферромагнетика и изменении его температуры.
Намагниченность
Для характеристики состояния намагниченного состояния магнетика используют вектор намагниченности ($\overrightarrow{J}$).
Намагниченностью ($\overrightarrow{J}$) называют физическую величину, которая равна:
\[\overrightarrow{J}=\frac{1}{\triangle V}\sum\limits_{\triangle V}{{\overrightarrow{p}}_{mi}(5)},\]где $\triangle V$ -- элементарный объем, $\overrightarrow{p_{mi}}$ -- магнитные моменты молекул, суммирование осуществляется по всем молекулам в объеме $\triangle V$. Из формулы (5) можно заключить, что:
\[p_m=\overrightarrow{J}dV\left(6\right).\]В несильных магнитных полях намагниченность диа- и парамагнетиках пропорциональна напряженности магнитного поля ($\overrightarrow{H}$):
\[\overrightarrow{J}=\varkappa {\mu }_0\overrightarrow{H\ }\left(7\right),\]где $\varkappa $ -- магнитная восприимчивость среды (магнетика).
Для парамагнетиков и диамагнетиков зависимость вектора намагниченности от напряженности магнитного поля линейна (рис.1).
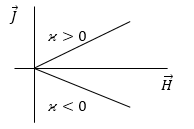
Рис. 1
У ферромагнетиков наблюдается явление гистерезиса (рис 2).
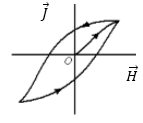
Рис. 2
Напряжённость магнитного поля
Когда магнетики отсутствуют, выполняется соотношение, которое описывает возникновение магнитного поля:
\[rot\overrightarrow{B}={\mu }_0\overrightarrow{j}\left(8\right).\]При наличии магнетиков поле порождается не только токами проводимости$\ (\overrightarrow{j)}$, но и молекулярными токами $(\overrightarrow{j_{mol})}$. Следовательно, (8) преобразуется к виду:
\[rot\overrightarrow{B}={\mu }_0\left(\overrightarrow{j}+\overrightarrow{j_{mol}}\right)={\mu }_0\overrightarrow{j}+rot\overrightarrow{J}\left(9\right).\]Задание: Из какого свойства магнитного поля следует соотношение для нормальной составляющей магнитного поля при переходе через границу раздела двух магнетиков: $B_{1n}=B_{2n}?$
Решение:
На границе раздела магнетиков в отсутствии токов проводимости выполняется теорема Гаусса:
\[\oint\limits_S{\overrightarrow{B}\overrightarrow{dS}=\int\limits_V{div}\overrightarrow{B}dV=0\ \left(1.1\right).}\]C другой стороны непосредственное вычисление потока дает нам:
\[\oint\limits_S{\overrightarrow{B}\overrightarrow{dS}=\ \left(1.2\right).}\]Следовательно, получаем, что $B_{2n}-B_{1n}$=0
Задание: На границе раздела магнетиков силовые линии магнитного поля преломляются. Докажите, что закон преломления линий $\overrightarrow{B}$ имеет вид $\frac{tg\alpha }{tg\beta }=\frac{{\mu }_1}{{\mu }_2}.$
Решение:
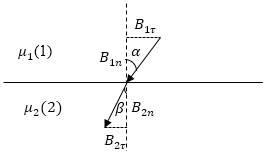
Рис. 3
Основой для решения задачи станет тот факт, что линии индукции магнитного поля ($\overrightarrow{В}$) проходят границу раздела двух магнетиков не прерываясь (рис.3). Количество линий приходящих к площадке $\triangle S$ из магнетика с номером (1) будет равно:
\[В_1\triangle S_1=В_1\triangle Scos\alpha \ \left(2.1\right).\]Количество линий выходящих из площадки $\triangle S$ в магнетик с номером (2) равно:
\[В_2\triangle S_2=В_2\triangle Scos\beta \ \left(2.2\right).\]Так как линии не претерпевают разрыва, то из количества должны быть одинаковы, то есть запишем, что:
\[В_1\triangle Scos\alpha =В_2\triangle Scosв\ \ \left(2.3\right),\]где
\[В_1cos\alpha =В_{1n},\ В_2cos\beta =В_{2n}\left(2.4\right).\]На границе магнетиков линии магнитной индукции терпят преломление, угол между нормалью к поверхности раздела и линией магнитной индукции изменяется ($\alpha \to \beta $). Из рис 1. следует, что
\[\frac{tg\alpha }{tg\beta }=\frac{В_{1\tau }}{В_{1n}}:\frac{В_{2\tau }}{В_{2n}}\left(2.5\right).\]А мы знаем, что:
\[\frac{В_{2\tau }}{В_{1\tau }}=\frac{{\mu }_2}{{\mu }_1},\ В_{1n}=В_{2n}\left(2.6\right),\ \]следовательно, подставляя граничные условия для составляющих вектора магнитной индукции в (2.5) получим закон преломления линий магнитной индукции:
\[\frac{tg\alpha }{tg\beta }=\frac{В_{1\tau }}{В_{2\tau }}\cdot \frac{В_{1n}}{В_{2n}}=\frac{{\mu }_1}{{\mu }_2}.\]Ответ: Мы получили искомый закон преломления:$\frac{tg\alpha }{tg\beta }=\frac{{\mu }_1}{{\mu }_2}.$











