Положение материальной точки на окружности определяется радиусом-вектором $ \overrightarrow {r}$, проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 1).
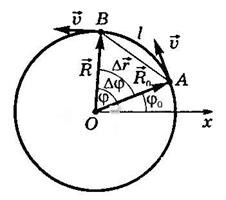
Рисунок 1. Радиус-вектор, перемещение, путь и угол поворота при движении точки по окружности
При этом движение тела по окружности можно однозначно описать с помощью таких кинематических характеристик, как угол поворота, угловая скорость и угловое ускорение.
За время ∆t тело, двигаясь из точки А в точку В, совершает перемещение $\triangle r$, равное хорде АВ, и проходит путь, равный длине дуги l. Радиус-вектор поворачивается на угол ∆$ \varphi $.
Угол поворота можно характеризовать вектором углового перемещения $d\overrightarrow{{\mathbf \varphi }}$, модуль которого равен углу поворота ∆$ \varphi $, а направление совпадает с осью вращения, причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора $d\overrightarrow{{\mathbf \varphi }}$.
Вектор $d\overrightarrow{{\mathbf \varphi }}$ называется аксиальным вектором (или псевдо-вектором), тогда как вектор перемещения $\triangle \overrightarrow{r}$ является полярным вектором (к ним также относятся векторы скорости и ускорения). Они отличаются тем, что полярный вектор кроме длины и направления имеет точку приложения (полюс), а аксиальный вектор имеет только длину и направление (ось - по латыни axis), но не имеет точки приложения. Векторы такого типа часто применяются в физике. К ним, например, относятся все вектора, являющиеся векторным произведением двух полярных векторов.
Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется средней угловой скоростью: $\left\langle \omega \right\rangle =\frac{\triangle \varphi }{\triangle t}$. В СИ единицей угловой скорости является радиан в секунду $( \frac {рад} {c})$.
Угловой скоростью вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:
\[\overrightarrow{{\mathbf \omega }}\left(t\right)={\mathop{lim}_{\triangle t\to 0} \frac{\triangle {\mathbf \varphi }}{\triangle t}=\frac{d\overrightarrow{{\mathbf \varphi }}}{dt}\ }\]При равномерном движении по окружности угловая скорость и модуль линейной скорости - величины постоянные: ${\mathbf \omega }=const$; $v=const$.
Учитывая, что $\triangle \varphi =\frac{l}{R}$, получаем формулу связи между линейной и угловой скоростью: $\omega =\frac{l}{R\triangle t}=\frac{v}{R}$. Угловая скорость также связана с нормальным ускорением: $a_n=\frac{v^2}{R}={\omega }^2R$
При неравномерном движении по окружности вектор угловой скорости является векторной функцией от времени $\overrightarrow{\omega }\left(t\right)={\overrightarrow{\omega }}_0+\overrightarrow{\varepsilon }\left(t\right)t$, где ${\overrightarrow{{\mathbf \omega }}}_0$ -- начальная угловая скорость, $\overrightarrow{{\mathbf \varepsilon }}\left(t\right)$ -- угловое ускорение. В случае равнопеременного движения, $\left|\overrightarrow{{\mathbf \varepsilon }}\left(t\right)\right|=\varepsilon =const$, и $\left|\overrightarrow{{\mathbf \omega }}\left(t\right)\right|=\omega \left(t\right)={\omega }_0+\varepsilon t$.
Опишите движение вращающегося твердого тела в случаях, когда угловая скорость изменяется согласно графикам 1 и 2, изображенным на рис.2.
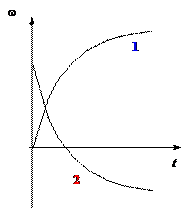
Рисунок 2.
Решение
Вращение бывает в двух направлениях - по часовой стрелке и против. С направлением вращения связан псевдовектор угла поворота и угловой скорости. Пусть положительным будем считать направление вращения по часовой стрелке.
Для движения 1 угловая скорость возрастает, но угловое ускорение $\varepsilon $=d$\omega $/dt (производная) уменьшается, оставаясь положительным. Следовательно, это движение является ускоренным по часовой стрелке с уменьшающимся по величине ускорением.
Для движения 2 угловая скорость уменьшается, затем достигает в точке пересечения с осью абсцисс нуля, а далее становится отрицательной и возрастает по модулю. Угловое ускорение отрицательно и уменьшается по модулю. Таким образом, сначала точка двигалась по часовой стрелке замедленно с уменьшающимся по модулю угловым ускорением, остановилась и стала вращаться ускоренно с уменьшающимся по модулю ускорением.
Найти радиус R вращающегося колеса, если известно, что линейная скорость $v_1$ точки, лежащей на ободе, в 2,5 раза больше линейной скорости $v_2$ точки, лежащей на расстоянии $r = 5 см$ ближе к оси колеса.
Решение
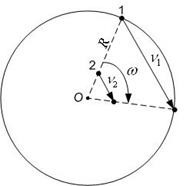
Рисунок 3.
Дано:
$$R_2 = R_1 - 5$$ $$v_1 = 2,5v_2$$ $$R_1 = ?$$Точки движутся по концентрическим окружностям, вектора их угловых скоростей равны, $\left|{\overrightarrow{\omega }}_1\right|=\left|{\overrightarrow{\omega }}_2\right|=\omega $ , следовательно, можно записать в скалярной форме:
\[v_1=\omega R_1; v_2=\omega R_2;\frac{v_1}{v_2}=\frac{\omega R_1}{\omega R_2}=\frac{R_1}{R_1-5}=2,5;;\ R_1=\frac{5\times 2,5}{1.5}=8,3\ см\ \ \]Ответ: радиус колеса R = 8,3 см











