Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
Различают пять видов движения твердого тела, и, соответсвенно, пять видов траекторий:
- Поступательному движению тела в кинематике соответствует прямолинейное движение материальной точки;
- вращательному движению тела соответствует движение материальной точки по окружности;
- плоскому движению тела соответствует движение материальной точки по плоскости;
- сферическому движению тела соответствует движение материальной точки по поверхности сферы;
- свободному движению тела соответствует движение материальной точки по произвольной траектории.
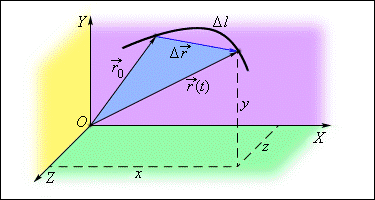
Рисунок 1
Определение положения точки с помощью координат x = x (t), y = y (t) и z = z (t) и радиус-вектора $\overrightarrow{r}\left(t\right)$ . $\overrightarrow{r_0\ }$-- радиус-вектор положения точки в начальный момент времени
Закон движения, задающий положение материальной точки в пространстве в любой момент времени, можно определять либо координатным способом, через зависимость координат от времени x = x (t), y = y (t), z = z (t), либо векторным способом, через зависимость от времени радиус-вектора $\overrightarrow{r}=\overrightarrow{r}\left(t\right)$, проведенного из начала координат к данной точке (рис. 1.1).
Перемещением тела $\overrightarrow{s}=\triangle \overrightarrow{r_{12}}=\overrightarrow{r_2}-\overrightarrow{r_1\ }$ называют направленный отрезок прямой, соединяющий начальную и конечную точки траетктории тела. Пройденный путь l равен длине траектории, пройденной телом за некоторое время t.
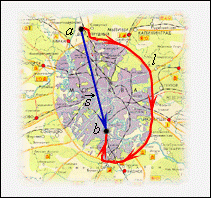
Рисунок 2
Пройденный путь $l$ и вектор перемещения $\overrightarrow{s}$ при кривoлинейном движении тела. $a$ и $b$ – начальная и конечная точки пути
Как видно из рис.2, при движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.
Перемещение - величина векторная. Это направленный отрезок.
Путь - скалярная величина. Это число.
Сумма двух последовательных перемещений из точки 1 в точку 2 и из точки 2 в точку 3 есть перемещение из точки 1 в точку 3 (рис. 3):
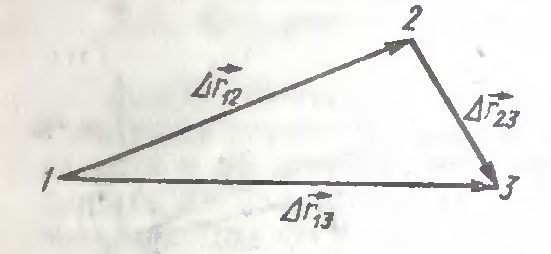
Рисунок 3. Сумма двух последовательных перемещений.
\[\triangle {\overrightarrow{r}}_{13}=\triangle {\overrightarrow{r}}_{12}+\triangle {\overrightarrow{r}}_{23}={\overrightarrow{r}}_2-{\overrightarrow{r}}_1+{\overrightarrow{r}}_3-{\overrightarrow{r}}_2={\overrightarrow{r}}_3-{\overrightarrow{r}}_1\]Если радиус-вектор материальной точки в момент времени t есть $\overrightarrow{r}$ (t), а в момент времени $t+\triangle t$ есть $\overrightarrow{r}$ (t$+\triangle t$) , то ее перемещение $\triangle \overrightarrow{r}$ за промежуток времени $\triangle t$ составит: $\triangle \overrightarrow{r}=\overrightarrow{r}$ (t$+\triangle t)-\overrightarrow{r}$ (t)
Перемещение $\triangle \overrightarrow{r}$ есть функция времени t: $\triangle \overrightarrow{r}=\triangle \overrightarrow{r}(t)$
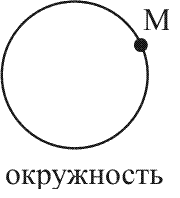
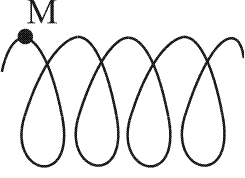
Летит самолет (рис. 4). Определить вид траектории точки М.
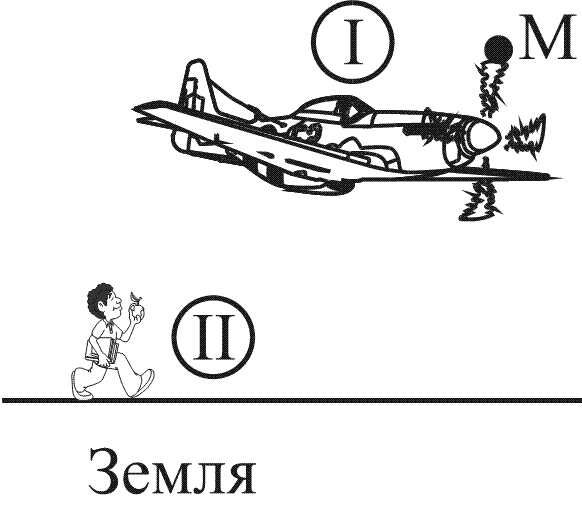
Рисунок 4
Решение.
В системе отсчета I («Самолет») траектория точки М - окружность.
В системе отсчета II («Земля») траектория точки М - спираль.
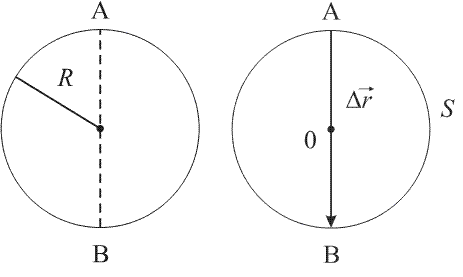
Материальная точка движется из положения А в В. Радиус окружности R = 1 м. Найти: S = ?, $| \triangle \overrightarrow{r}|$ = ?
Решение.
При своем движении из т. А в т. В материальная точка проходит путь, равный половине длины окружности: S = $\pi $R; S = 3,14 1 м = 3,14 м.
Перемещение $\triangle \overrightarrow{r}$ -- это вектор, соединяющие начальное положение материальной точки (т. А) с ее конечным положением (т. В):
|$\triangle \overrightarrow{r}$| = 2R = 2 1 м = 2 м.
Ответ: S = 3,14 м; |$\triangle \overrightarrow{r}$| = 2 м.











