Пусть за время $\Delta $t движущаяся точка перешла из положения А в положение В (рис. 1.).
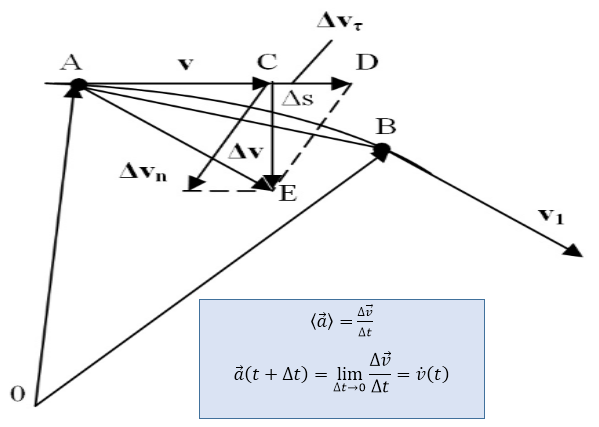
Рисунок 1. Мгновенное ускорение и его составляющие
Вектор $\overrightarrow{v}$ задает скорость точки в положении А. В положении В точка приобрела скорость, отличную от $\overrightarrow{v}$ как по величине, так и по направлению и стала равной $\overrightarrow{v_1}=\overrightarrow{v}+\triangle \overrightarrow{v}$ . Перенесем вектор $\overrightarrow{v_1}$ в точку А и найдем $\Delta $$\overrightarrow{v}$.
Мгновенным ускорением, или просто ускорением материальной точки в момент времени t, называется предел среднего ускорения $\left\langle \overrightarrow{a}\right\rangle =$ $\frac{\triangle \overrightarrow{v}}{\triangle t}$ при бесконечно малом приращении времени: $\overrightarrow{a}\left(t+\triangle t\right)={\mathop{lim}_{\triangle t\to 0} \frac{\triangle \overrightarrow{v}}{\triangle t}=\dot{v}\left(t\right)\ }$.
Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.
Разложим вектор $\Delta $$\overrightarrow{v}$ на две составляющие. Для этого из точки А по направлению скорости $\overrightarrow{v}$ отложим вектор AD, по модулю равный ${\overrightarrow{v}}_1$. Тогда вектор CD, равный $\Delta $${\overrightarrow{v}}_{\tau }$, определяет изменение скорости по модулю (величине) за время $\Delta $t, т.е. $\Delta $${\overrightarrow{v}}_{\tau }={\overrightarrow{v}}_1-\overrightarrow{v}$. Вторая же составляющая вектора $\triangle \overrightarrow{v}$ характеризует изменение скорости на время $\Delta $t по направлению - $\Delta $${\overrightarrow{v}}_n$. Составляющая ускорения, определяющая изменение скорости по величине, называется тангенциальным ускорением ${\overrightarrow{a}}_{\tau }$. Численно она равна первой производной по времени от модуля скорости: $a_{\tau }=\frac{dv}{dt}$.
Найдем вторую составляющую ускорения, называемую нормальным ускорением ${\overrightarrow{a}}_n$. Допустим, что точка В достаточно близка к точке А, поэтому путь $\Delta $s можно считать дугой окружности некоторого радиуса r, мало отличающегося от хорды АВ. Из подобия треугольников АОВ и ЕАD следует, что $\frac{{\triangle v}_n}{AB}=\frac{v_1}{r}$, или, учитывая, что $AB\approx \triangle s=v\triangle t$, получим: $\frac{{\triangle v}_n}{v\triangle t}=\frac{v_1}{r}$, откуда $\frac{{\triangle v}_n}{\triangle t}=\frac{vv_1}{r}$. Учитывая, что при бесконечно малом приращении времени $v_1\to v$, и переходя к пределу, получим: $a_n={\mathop{lim}_{\triangle t\to 0} \frac{{\triangle v}_n}{\triangle t}\ }=\frac{v^2}{r}$.
Нормальное ускорение характеризует быстроту изменения скорости по направлению и направлено к центру кривизны траектории по нормали. Его называют также центростремительным ускорением. Полное мгновенное ускорение есть геометрическая сумма тангенциальной и нормальной составляющих: $\overrightarrow{a}={\overrightarrow{a}}_{{\mathbf \tau }}+{\overrightarrow{a}}_n$
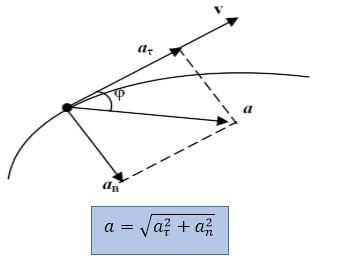
Рисунок 2. Полное ускорение
Модуль полного мгновенного ускорения $a=\sqrt{a^2_{\tau }+a^2_n}$.
Направление полного ускорения определяется углом $\varphi $ между векторами ${\overrightarrow{a}}_{{\mathbf \tau }}$ и $\overrightarrow{a}$. Как видно из рис. 2, $\varphi =arctg\frac{a_n}{a_{\tau }}$.
Движение материальной точки может быть следующих видов:
- ${\overrightarrow{a}}_{{\mathbf \tau }} = 0$, ${\overrightarrow{a}}_n = 0$ -- прямолинейное равномерное движение (s=vt);
- ${\overrightarrow{a}}_{{\mathbf \tau }} = const \neq 0$, ${\overrightarrow{a}}_n= 0$ -- прямолинейное равнопеременное движение.
- ${\overrightarrow{a}}_{{\mathbf \tau }} = f(t)$, ${\overrightarrow{a}}_n$ $= 0$ -- прямолинейное движение с переменным ускорением;
- ${\overrightarrow{a}}_{{\mathbf \tau }} = 0$, ${\overrightarrow{a}}_n = const$ -- равномерное движение по окружности;
- ${\overrightarrow{a}}_{{\mathbf \tau }} = 0$, ${\overrightarrow{a}}_n \neq 0$ -- равномерное криволинейное движение;
- ${\overrightarrow{a}}_{{\mathbf \tau }} = const$, ${\overrightarrow{a}}_n \neq 0$ -- криволинейное равнопеременное движение;
- ${\overrightarrow{a}}_{{\mathbf \tau }}$ = $f(t)$, ${\overrightarrow{a}}_n \neq 0$ -- криволинейное движение с переменным ускорением.
Тело движется равноускоренно с начальной скоростью $v_0 = 5 м/с$. Определить мгновенное ускорение тела момент времени $t=7 с$, если его скорость в этот момент составила $26 м/с$.
Решение
\[a=\left\langle a\right\rangle =\frac{\triangle v}{\triangle t}=\frac{26-5}{7}=21\ м/c^2\]Материальная точка движется по кривой с постоянным радиусом кривизны $R = 3 м$. Линейная скорость точки описывается уравнением $v=2t+t^2$. Найти мгновенное ускорение точки в момент $t = 3 c$. Определить тип движения точки.
Решение
Модуль полного мгновенного ускорения $a=\sqrt{a^2_{\tau }+a^2_n}$
Тангенциальное ускорение $a_{\tau }\left(3\right)=\frac{dv}{dt}=2+2t=2+6=8\ м/с^2$
Скорость $v\left(5\right)=2\times 3+3^2=15\ м/c$
Нормальное ускорение $a_n\left(3\right)=\frac{v^2}{r}=\frac{{15}^2}{3}=75$
Полное мгновенное ускорение $a\left(3\right)=\sqrt{8^2+{75}^2}=75.43\ м/с^2$
Точка равномерно движется по окружности радиусом 3 м











