Историческая справка
Закон Кулона входит в число основных экспериментальных фактов, находящихся в основании теории б электричестве. Этот закон для определения силы взаимодействия точечных зарядов $q_1\ $ и $q_2$, которые находятся на расстоянии $r$, имеет вид:
где ${\varepsilon }_0=8,8\cdot {10}^{-12}\frac{Ф}{м}$.
Этот закон установлен Ш. Кулоном в 1785 г. экспериментально. Кулон измерял силы взаимодействия заряженных тел. Точность опытов была плохой, только аналогии с силами тяготения дала уверенность в том, что закон в виде (1) справедлив. С результатами эксперимента, обычно сравнивают следствия из закона Кулона, и на этой основе делается вывод о точности и границах применения данного закона. Первая проверка закона была проведена Кавендишем за 13 лет до Кулона. Кавендиш работ не публиковал, но надо отметить, что его метод был более точным, чем эксперименты Кулона. Позднее опыты по проверке закона Кулона проводил Максвелл. Эти опыты подтвердили справедливость закона Кулона с большой точностью. В соответствии с современными представлениями электромагнитные взаимодействия осуществляются посредством фотонов. Вследствие чего вопрос о справедливости закона Кулона сводится к вопросу о равенстве массы фотона нулю. Все частицы обладают корпускулярными и волновыми свойствами. Энергия фотона (${\varepsilon }_{\nu }=h\nu $) и ${\varepsilon }_{\nu }=m_{\nu }c^2$, где $m_{\nu }$ - масса фотона, $h$ - постоянная Планка. Масса $m_{\nu}$ больше массы покоя, если у фотона масса отлична от нуля. Следовательно, если найти верхний предел для $m_{\nu }$, получим ограничение для массы покоя фотона. Если существование электромагнитных волн с большой длиной волны (а лучше бесконечной) доказать, то можно утверждать, что $m_{\nu }$ очень мало. Наиболее длинные электромагнитные волны, которые удалось наблюдать на сегодняшний момент, образуются в виде стоячих волн в пространстве между поверхностью Земли и ионосферой. Они носят имя Шумана, а точнее называются резонансами Шумана. Минимальный резонанс Шумана соответствует частоте $\nu $=8Гц. С учетом расстояния от поверхности Земли было получено, что $m_{\nu }
Для малых расстояний закон Кулона проверяется в экспериментах, связанных с элементарными частицами. Уже опыты Резерфорда доказали, что закон Кулона справедлив с большой точностью на расстоянии ${10}^{-15}м$.
До работ Фарадея закон Кулона трактовался с позиций дальнодействия, то есть считалось, что одно тело действует на другое без посредников (действие на расстоянии). В первой половине 18 века сложился другой взгляд на механизм взаимодействия, в соответствии с которым существует посредник, осуществляющий непрерывную передачу сил.(теория близкодействия). Поначалу таким посредником назначили, так называемый Мировой эфир. Состояние которого характеризовали некоторыми механическими свойствами. Попытка математического описания механической картины передачи электрических взаимодействий была сделана Максвеллом. Он пытался представить электромагнитные силы в виде механических сил, которые вызываются натяжением и давлением в эфире. Позже Максвелл перешел к феноменологической формулировке взаимодействия и охарактеризовал состояние среды с помощью векторов: напряженности электростатического поля ($\overrightarrow{E}$), электрического смещения ($\overrightarrow{D}$), напряженности магнитного поля ($\overrightarrow{H}$), магнитной индукции ($\overrightarrow{B}$), которым не дал никакой механической интерпретации. В 1864 г. Максвелл сформулировал уравнения электромагнитного поля (уравнения Максвелла). Надежда на механическое толкование электромагнитных взаимодействий умерла. Поле стало основной сущностью, посредством которого осуществляется электромагнитное взаимодействие. Оно характеризуется величинами, которые не могут интерпретироваться в рамках механики. После того как Герц записал уравнения Максвелла в современном виде стало очевидно, что поле существует в пространстве и времени наряду с материей.
Полевая трактовка закона Кулона
Пусть мы имеем два точечных заряда $q_1\ (точка\ 1)\ $ и $q_2$(точка 2).Тогда ${\overrightarrow{F}}_{12}$- сила, с которой заряд $q_1$ действует на заряд $q_2$. ${\overrightarrow{F}}_{21}$- сила, с которой заряд $q_2$ действует на заряд $q_1$. ${\overrightarrow{r}}_{12}$- вектор из точки (1) в точку (2), ${\overrightarrow{r}}_{21}$ - вектор из точки (2) в точку (1). Исходя из принятых нами обозначений, запишем закон Кулона:
По своему физическому содержанию формулы (2) и (3) различны. Они определяют силы, которые действуют на второй (2) и первый (3) заряды, то есть описывают силы в разных точках пространства. Механизм же возникновения этих сил одинаков. Заряды вокруг себя создают электрическое поле. Это поле принято характеризовать напряженностью ($\overrightarrow{E}$). Напряженностью электрического поля является физическая величина, которая равна отношению силы, с которой действует поле на положительный заряд, помещенный в данную точку поля к заряду. Соответственно, с учетом (2,3), запишем:
Соответственно:
Формула (4) описывает напряженность электрического поля, которое образуется зарядом $q_1.$ Формула (5) характеризует силу, с которой поле с напряженностью ${\overrightarrow{E}}_2$ действует на заряд, который находится в точке поля. Действие одного заряда на другой делится на:
- Точечный заряд создает вокруг себя электрическое поле, напряженность которого равна: \[\overrightarrow{E}=\frac{1}{4\pi {\varepsilon }_0}\frac{q}{r^2}\frac{\overrightarrow{r}}{r}\ \left(8\right),\]
- На точечный заряд q, который находится в точке поля с напряженностью $\overrightarrow{E}$, действует сила равная: \[\overrightarrow{F}=q\overrightarrow{E}\ \left(9\right).\]
где $\overrightarrow{r}$- радиус -- вектор, проведенный из точки нахождения заряда до точки, в которой определяется напряженность.
Эти два утверждения дают полевую трактовку Закона Кулона.
Если имеется несколько источников поля (количество зарядов $N$), то результирующую силу, действующую на пробный заряд $q$ можно найти как:
\[\overrightarrow{F}=\sum\limits^N_{i=1}{\overrightarrow{F_{ia}}}\left(10\right),\]где $\overrightarrow{F_{ia}}$ -- сила, с которой N зарядов действуют на заряд $q$.
Закон Кулона в формуле (1) записан для вакуума, если мы имеем дело с какой-то средой, ее диэлектрические свойства характеризует диэлектрическая проницаемость среды ($\varepsilon $), тогда уравнение (1) примет вид:
\[\overrightarrow{F}=\frac{1}{4\pi {\varepsilon \varepsilon }_0}\frac{q_1q_2\overrightarrow{r}}{r^3}\ \left(11\right).\]Задание: Три одинаковых точечных заряда величиной $q$ поместили в вершинах равностороннего треугольника. Найдите величину точечного заряда $Q$, который надо поместить в центр масс треугольника, чтобы система находилась в состоянии равновесия.
Решение:
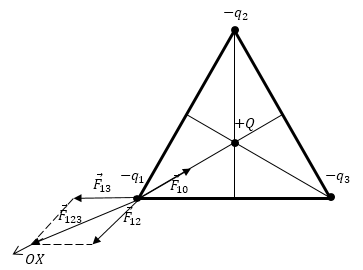
Рис. 1
Для определенности допустим, что заряды в вершинах треугольника отрицательные, тогда на пересечении медиан (в центре масс) положительный.
Рассмотрим силы, которые действуют на заряд ${-q}_1$. Это будут три силы Кулона, две -- отталкивания, со стороны зарядов в вершинах и одна -- притяжения со стороны «центрального». Тогда условие равновесия сил запишем в виде:
\[\overrightarrow{F_{12}}+\overrightarrow{F_{13}}+\overrightarrow{F_{10}}=0\ \left(1.1\right).\]Выберем ось OX, как указано на рис.1, найдем проекцию уравнения (1) на эту ось:
\[F_{12}{cos \left(\frac{\alpha }{2}\right)\ }+F_{13}{cos \left(\frac{\alpha }{2}\right)\ }-F_{10}=0\ \left(1.2\right),\]где $\alpha $- угол треугольника (так как треугольник равносторонний, следовательно, $\alpha =60{}^\circ $).
Так как по условию задачи треугольник равносторонний, заряды в вершинах одинаковые и равны q, то $F_{12}=F_{13}$, а по закону Кулона:
\[F_{12}=F_{13}=\frac{q^2}{4 \pi \varepsilon \varepsilon_0a^2}\ \left(1.3\right),\]где a -- сторона треугольника. Для силы $F_{10}$ по закону Кулона получим:
\[F_{10}=\frac{qQ}{4\pi \varepsilon \varepsilon_0r^2}\ \left(1.4\right).\]В таком случае выражение (1.2) запишем в виде:
\[\frac{2q^2}{4\pi {\varepsilon \varepsilon }_0a^2}{cos \left(\frac{\alpha }{2}\right)\ }=\frac{qQ}{4\pi {\varepsilon \varepsilon }_0r^2}\ \left(1.5\right),\]где точка пересечения медиан делит их в соотношении 2:1, если считать от вершины, следовательно:
\[r=\frac{2}{3}{acos \left(\frac{\alpha }{2}\right)\ }\left(1.6\right).\]Подставляем (1.6) в (1.5) выражаем $Q$, получаем:
\[Q=\frac{8qcos^3\left(\frac{б}{2}\right)}{9}\]Ответ: $Q=\frac{8qcos^3\left(\frac{\alpha }{2}\right)}{9}$ (Кл).
Задание: Положительный точечный заряд 1 Кл находится на плоскости XOY в точке, которая определена радиус - вектором$\overrightarrow{{\ r}_1}=4\overrightarrow{i}+6\overrightarrow{j}$,(м) где $i$ и $j$ -- орты осей. Найдите модуль напряженности электрического поля E в точке с радиус-вектором $\overrightarrow{{\ r}_2}=16\overrightarrow{i}-\overrightarrow{j}\ (м)$.
Решение:
Найдем разность векторов $\overrightarrow{{\ r}_2}$-$\overrightarrow{{\ r}_1}$, получим:
\[\overrightarrow{{\ r}_2}-\overrightarrow{{\ r}_1}=12\overrightarrow{i}-\overrightarrow{7j}\ \left(2.1\right).\]Из закона Кулона выражение для напряженности электростатического поля может быть записано как:
\[E=\frac{1}{4\pi {\varepsilon }_0}\frac{q}{r^2}=k\frac{q}{r^2}\ \left(2.2\right),\]где $k=9•{10}^9\frac{Нм^2}{{Кл}^2}$
Найдем $r$, получим:
\[r=\left|\overrightarrow{{\ r}_2}-\overrightarrow{{\ r}_1}\right|=\sqrt{{12}^2+7^2}\approx 13,89\ (м)\]Вычислим напряженность (модуль), получим:
\[E=9\cdot {10}^9\frac{1}{193}\approx 4,7{\cdot 10}^7\ \left(\frac{В}{м}\right).\]Ответ: Напряженность поля в заданной точке $4,7{\cdot 10}^7\frac{В}{м}$.











