Что такое вектор электрической индукции
Вектором электрической индукции (или вектором электрического смещения) ($\overrightarrow{D}$) называют физическую величину, которая определяется в системе СИ как:
\[\overrightarrow{D}={\varepsilon }_0\overrightarrow{E}+\overrightarrow{P}\ \left(1\right),\]где ${\varepsilon }_0$ -- электрическая постоянная, $\overrightarrow{E}$ -- вектор напряженность, $\overrightarrow{P}$ -- вектор поляризации.
В СГС вектор электрического смещения определен как:
\[\overrightarrow{D}=\overrightarrow{E}+4\pi \overrightarrow{P}\ \left(2\right).\]Вектор $\overrightarrow{D}$ не является чисто полевым вектором, так как он учитывает поляризованность среды. Этот вектор связан с объемной плотностью заряда соотношением:
\[div\overrightarrow{D}=\rho \left(3\right).\]Из (3) мы видим, что единственным источником $\overrightarrow{D}$ являются свободные заряды, на которых данный вектор начинается и заканчивается. В точках, где свободные заряды отсутствуют, вектор электрической индукции непрерывен. Изменение напряженности поля, которые вызваны наличием связанных зарядов, учитываются в самом векторе $\overrightarrow{D}$.
Связь вектора напряженности и вектора электрического смещения
Связь вектора напряженности и вектора электрического смещения, если среда изотропна, еще можно записать как:
\[\overrightarrow{D}=\left({\varepsilon }_0\overrightarrow{E}+{\varepsilon }_0\varkappa \overrightarrow{E}\right)=\left({\varepsilon }_0+{\varepsilon }_0\varkappa \right)\overrightarrow{E}=\varepsilon {\varepsilon }_0\overrightarrow{E}\left(4\right),\]где $\varepsilon $ -- диэлектрическая проницаемость среды.
Использование вектора $\overrightarrow{D}$ существенно облегчает анализ поля при наличии диэлектрика. Так, например теорема Остроградского - Гаусса в интегральном виде при наличии диэлектрика может быть записана как:
\[\int\limits_S{\overrightarrow{D}\cdot d\overrightarrow{S}=Q\left(5\right).}\]При переходе через границу раздела двух диэлектриков для нормальной составляющей вектора $\overrightarrow{D}$ можно записать:
\[D_{2n}-D_{1n}=\sigma \ \left(6\right).\]или
\[\overrightarrow{n_2}\left(\overrightarrow{D_2}-\overrightarrow{D_1}\right)=\sigma \ \left(7\right),\]где $\sigma $ -- поверхностная плотность распределения зарядов на границе диэлектриков. $\overrightarrow{n_2}$ -- нормаль, которая проведена в сторону второй среды.
Для тангенциальной составляющей:
\[D_{2\tau }=\frac{{\varepsilon }_2}{{\varepsilon }_1}D_{1\tau }\left(8\right).\]Единицей измерения в системе СИ вектора электрической индукции служит $\frac{Кл}{м^2}.$
Поле вектора $\overrightarrow{D}$ можно изображать с помощью линий электрического смещения. Направление и густота определяются аналогично линиям вектора напряженности. Однако в отличие от вектора $\overrightarrow{E}$ линии вектора электрической индукции начинаются и заканчиваются только на свободных зарядах.
Задание: Пластины плоского конденсатора имеют заряд q. Как изменится вектор электрической индукции, если пространство между пластинами сначала было заполнено воздухом, а за тем диэлектриком с диэлектрической проницаемостью $\varepsilon \ne {\varepsilon }_{vozd}$.
Решение:
Пусть поле в конденсаторе в первом случае характеризуется вектором смещения (${\varepsilon }_{vozd}=1$):
\[\overrightarrow{D_1}={\varepsilon }_{vozd}{\varepsilon }_0\overrightarrow{E_1}={\varepsilon }_0\overrightarrow{E_1}\left(1.1\right).\]Заполним пространство между пластинами конденсатора однородным и изотропным диэлектриком. Под действием поля в конденсаторе диэлектрик поляризуется. На его поверхности появляются связанные заряды с плотностью (${\sigma }_{sv}$). Они создают дополнительное поле, напряженность которого равна:
\[E'=\frac{{\sigma }_{sv}}{{\varepsilon }_0}\left(1.2\right).\]Векторы поля $\overrightarrow{E'}$ и $\overrightarrow{E_1}$ направлены в противоположные стороны, при чем:
\[E_1=\frac{\sigma }{{\varepsilon }_0}\ \left(1.3\right).\]Результирующее поле в присутствии диэлектрика можно записать как:
\[E=E_1-E'=\frac{\sigma }{{\varepsilon }_0}-\frac{{\sigma }_{sv}}{{\varepsilon }_0}=\frac{1}{{\varepsilon }_0}\left(\sigma -{\sigma }_{sv}\right)\left(1.4\right).\]Зная, что плотность связанных зарядов можно найти как:
\[{\sigma }_{sv}=\varkappa {\varepsilon }_0E\ \left(1.5\right).\]Подставим (1.5) в (1.4), получим:
\[E=E_1-\varkappa E\ \left(1.6\right).\]Выразим из (1.6) напряженность поля E, получим:
\[E=\frac{E_1}{1+\varkappa }=\frac{E_1}{\varepsilon }\ \left(1.7\right).\]Следовательно, вектор электрической индукции в диэлектрике равен:
\[D=\varepsilon {\varepsilon }_0\frac{E_1}{\varepsilon }={\varepsilon }_0E_1=D_1.\]Ответ: Вектор электрической индукции не изменится.
Задание: В зазор между разноименно заряженными пластинами внесли пластину из диэлектрика с диэлектрической проницаемостью $\varepsilon$, которая не несет свободных зарядов. Штриховой линией на рисунке изображена замкнутая поверхность (рис.1). Чему равен поток вектора электрической индукции ($Ф_D$) через эту поверхность?
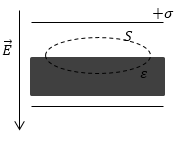
Рис. 1
Решение:
Поток вектора электрического смещения ($Ф_D$) через замкнутую поверхность $S$ равен:
\[Ф_D=\int\limits_S{\overrightarrow{D}\cdot d\overrightarrow{S}\left(2.1\right).}\]С другой стороны по теореме Остроградского -- Гаусса $Ф_D$ равен суммарному свободному заряду, который находится внутри заданной поверхности. По условию нашей задачи свободных зарядов в диэлектрике и в пространстве между пластинами конденсатора, которое не занято диэлектриком свободных зарядов нет, следовательно, поток вектора электрической индукции равен нулю.
Ответ: $Ф_D$=0.
Задание: На рисунке 2 изображена замкнутая поверхность $S$ которая проходит так, что захватывает часть пластины изотропного диэлектрика. При этом известно, что поток вектора электрической индукции через эту поверхность равен нулю, а поток вектора напряженности больше нуля. Какие выводы можно сделать?
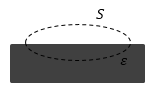
Рис. 2
Решение:
Если по условию задачи, поток вектора электрического смещения ($Ф_D$) через замкнутую поверхность равен нулю:
\[Ф_D=0\left(3.1\right),\ \]а он по теореме Остроградского -- Гаусса $Ф_D$ равен суммарному свободному заряду, который находится внутри заданной поверхности, следовательно, то внутри этой поверхности нет свободных зарядов:
\[Ф_D=\int\limits_S{\overrightarrow{D}\cdot d\overrightarrow{S}=Q=0\left(3.2\right).}\]Но при этом сказано, что отличен от нуля поток вектора напряженности, но его поток равен сумме зарядов и свободных и связанных, следовательно, в диэлектрике присутствуют связанные заряды.
Ответ: Свободных зарядов нет, связанные заряды есть и их сумма положительна.











