Теорема с диэлектриками
Влияние диэлектриков на электрическое поле сводится к ответному действию возникающих в поле поляризационных зарядов. Поэтому теорему Остроградского -- Гаусса для тел в вакууме можно трансформировать, добавив к свободным зарядам поляризационные заряды и получить теорему с диэлектриками. В таком случае теорема Остроградского -- Гаусса примет вид в системе СИ:
где $q_{jsv}$ -- связанные заряды, $q_i$ -- свободные заряды, $Ф_E$ -- поток вектора напряженности электрического поля.
Использование вектора электрического смещения ($\overrightarrow{D})$ существенно облегчает анализ поля при наличии диэлектрика. Так, например, теорема Остроградского -- Гаусса в интегральном виде при наличии диэлектрика может быть записана как:
\[\oint\nolimits_S{\overrightarrow{D}\cdot d\overrightarrow{S}}=\sum\limits^N_{i=1}{q_i=}Q\left(2\right),\]где $Q$- суммарный свободный заряд, который находится внутри объема, который ограничен поверхностью S.
Поток вектора $\overrightarrow{D}$ через замкнутую поверхность определен только свободными зарядами. В вакууме векторы $\overrightarrow{D}$ и $\overrightarrow{E}$ совпадают.
В дифференциальной форме выражение (2) принимает следующий вид:
\[div\overrightarrow{D}=\rho \ \left(3\right),\]где $\rho $ -- объемная плотность свободных зарядов. Теорема Остроградского - Гаусса в виде (2) и (3) справедлива не только в электростатике, она выполняется и для переменных полей. Данная теорема является составной частью системы уравнений Максвелла.
Теорема Остроградского -- Гаусса в дифференциальной форме
Вспомним определение вектора электрической индукции:
\[\overrightarrow{D}={\varepsilon }_0\overrightarrow{E}+\overrightarrow{P}\ \left(4\right),\]где ${\varepsilon }_0$ -- электрическая постоянная, $\overrightarrow{E}$ -- вектор напряженность, $\overrightarrow{P}$ -- вектор поляризации. Подставим (4) в выражение (3), получим:
\[div\overrightarrow{D}=div\left({\varepsilon }_0\overrightarrow{E}+\overrightarrow{P}\right)={\varepsilon }_0div\overrightarrow{E\ }+div\overrightarrow{P\ }\left(5\right).\]Следовательно, если использовать теорему Остроградского -- Гаусса в дифференциальном виде, то можно записать:
\[div\overrightarrow{E\ }=\frac{1}{{\varepsilon }_0}\left(\rho -div\overrightarrow{P\ }\right)\left(6\right).\]Но для вектора напряженности также можно записать теорему Остроградского -- Гаусса в дифференциальной форме в присутствии диэлектрика, она будет выглядеть как:
\[div\overrightarrow{E\ }=\frac{1}{{\varepsilon }_0}\left(\rho +{\rho }_{sv}\right)\left(7\right),\]где ${\rho }_{sv}$ -- плотность связанного заряда. В таком случае, используя (7) и (6), получим:
\[div\overrightarrow{P\ }=-\frac{1}{\varepsilon_0}с_{sv}\ \left(8\right).\]Теорема Остроградского -- Гаусса для вектора электрического смещения в диэлектрике имеет такой же вид, как для напряженности в вакууме. Следовательно, все математические соотношения, которые были получены для $\overrightarrow{E\ }$ поля в вакууме, имеют такой же вид для однородного диэлектрика при замене напряженности электрического поля на вектор $\overrightarrow{D\ }.$
Задание: Диэлектрический шар, диэлектрическая проницаемость которого ${\varepsilon }_1$ равномерно заряжен по объему с постоянной плотностью заряда $\rho $. Находится шар в среде с диэлектрической проницаемостью ${\varepsilon }_2$. Нарисуйте график зависимости напряженности поля шара от расстояния от его центра.
Решение:
Поле, которое создает шар, который дан в условиях задачи, имеет сферическую симметрию.
Рассмотрим поле внутри шара ($r\le R$). Для того, чтобы найти $E(r)$ выберем сферическую поверхность, радиус которой меньше радиуса сферы. Из теоремы Остроградского -- Гаусса имеем:
\[E\cdot S=\frac{q}{{\varepsilon }_1{\varepsilon }_0}\left(1.1\right),\]где $S$ -- площадь поверхности сферы, которую мы выделили, следовательно:
\[S=4\pi r^2\left(1.2\right).\]при этом заряд, который находится внутри выделенной сферы, мы можем найти как:
\[q=\rho V=\rho \frac{4}{3}\pi r^3\left(1.3\right).\]В таком случае напряженность поля внутри шара ($r\le R$) будет изменяться в соответствии с:
\[E\cdot 4\pi r^2=\frac{\rho \frac{4}{3}\pi r^3}{{\varepsilon }_1{\varepsilon }_0}\left(1.4\right),\] \[E=\frac{\rho r}{3{\varepsilon }_1{\varepsilon }_0}\ \left(1.5\right).\]Рассмотрим поле вне шара ($r\ge R$). Для того, чтобы найти E(r) выберем сферическую поверхность, радиус которой больше радиуса сферы. Из теоремы Остроградского -- Гаусса имеем:
\[E\cdot S=\frac{q}{{\varepsilon }_2{\varepsilon }_0}\left(1.6\right),\]где $S$ -- площадь поверхности сферы, которую мы выделили, следовательно:
\[S=4\pi r^2\left(1.7\right).\]Но мы помним, что в (1.7) $r\ge R$. При этом заряд, который находится внутри выделенной сферы, мы можем найти как:
\[q=\rho V=\rho \frac{4}{3}\pi R^3\left(1.8\right).\]Подставляем площадь из (1.7) и заряд из (1.8) в (1.6), получаем:
\[E\cdot 4\pi r^2=\frac{\rho \frac{4}{3}\pi R^3}{{\varepsilon }_2{\varepsilon }_0}\left(1.9\right).\] \[E=\frac{\rho R^3}{3{\varepsilon }_2{\varepsilon }_0r^2}.\]В результате мы получили:
\[\left\{ \begin{array}{c} E=\frac{\rho r}{3{\varepsilon }_1{\varepsilon }_0}\ при\ r\le R, \\ E=\frac{\rho R^3}{3{\varepsilon }_2{\varepsilon }_0r^2}\ при\ r\ge R. \end{array} \right.\]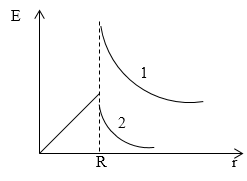
Рис. 1
Ответ: Рис. 1 графики, которые требовалось изобразить. Внутри шара напряженность растет прямо пропорционально расстоянию от центра шара. Вне шара $E\sim \frac{1}{r^2}$. На границе двух диэлектриков напряжённость испытывает разрыв. Причем, кривая с номером 1 соответствует ${\varepsilon }_1>{\varepsilon }_2$, кривая с номером 2 ${\varepsilon }_1
Задание: В центре воображаемой сферы находится точечный заряд. Изменится ли поток вектора напряженности через эту поверхность, если, 1)все пространство сферы заполнить однородным и изотропным диэлектриком, 2) заменить сферическую поверхность на кубическую?
Решение:
1) В соответствии с теоремой Остроградского -- Гаусса поток вектора напряженности через поверхность сферы в пространстве с диэлектриком будет равен:
\[Ф_E=\oint\limits_S{\overrightarrow{E}d\overrightarrow{S}}=\frac{1}{{\varepsilon }_0}(q+\sum\limits^K_{j=1}{q_{jsv}})\left(2.1\right),\]где $q_{jsv}$ -- связанные заряды, которые вызваны поляризацией диэлектрика полем одиночного заряда, $q$ -- свободный заряд, который находится в центре сферы.
В соответствии с теоремой Остроградского -- Гаусса поток вектора напряженности через поверхность сферы в пространстве без диэлектрика будет равен:
\[Ф_E=\oint\limits_S{\overrightarrow{E}d\overrightarrow{S}}=\frac{1}{{\varepsilon }_0}q\ \left(2.2\right).\]2) Так как поле создается точечным свободным зарядом, то при замене формы поверхности поток вектора напряженности не изменится, так как он равен величине заряда, который находится внутри поверхности.
Ответ: 1) Изменится. 2) Не изменится.












