Роль энергии электрического поля
Перемещение заряженных тел в электрическом поле сопровождается изменением энергии данного поля (W) и работой (A) пондемоторных сил поля. Если при этом не происходит превращений других форм энергии, то работа механических сил в поле совершается за счет изменения энергии поля ($\delta W$). Причем выполняется соотношение:
Получается, что зная изменение энергии электрического поля можно найти работу пондемоторных сил и соответственно, сами силы. Формула (1) показывает, что энергия электрического поля W играет роль, аналогичную потенциальной энергии в механике.
Работа пондемоторных сил
Для того, чтобы перенести заряд $dq$ в точку с потенциалом $\varphi $, необходимо совершит работу ($\delta A$) равную:
Работу пондемоторных сил при перемещении системы зарядов можно найти как:
Допустим, что конфигурация системы характеризуется параметром ${\xi }_i$, то обобщенной силой, которая связана с этим параметром будет величина $F_i,\ $такая, что $F_i$d$\ {\xi }_i$ -- работа которую выполняет система при изменении параметра ${\xi }_i$ на d$\ {\xi }_i$. При этом по закону сохранения имеем:
Если в системе заряд постоянен, то выражение (4) примет вид:
где ${\left(dW\right)}_q$- зависит только от ${\xi }_i$, следовательно:
Сравним уравнения (5) и (6), сделаем вывод, что:
где индекс $q$ указывает, что сила находится при постоянном заряде. Для того чтобы использовать формулу (7), необходимо, чтобы $W$ была выражена как функция от зарядов и параметров $\xi_i$.
Силу можно выразить при постоянном потенциале ($\varphi =const$). Однако необходимо учесть, что разность потенциалов на обкладках может оставаться постоянной при изменении расстояния между обкладками только, если эта разность поддерживается внешними силами, которые совершают изменение. Для этого энергию выразим как:
В таком случае приращение энергии ${\left(dW\right)}_{\varphi }$ равно:
Получаем:
где индекс $\varphi $ показывает, что частная производная вычисляется при постоянном потенциале.
Для того, чтобы использовать формулу (11), необходимо, чтобы W была выражена как функция от потенциалов ${\varphi }_i$ и параметров ${\xi }_i$.
Задание: Вычислите силу, с которой пластины плоского конденсатора притягиваются друг к другу при постоянном заряде и постоянном потенциале. Сравните полученные результаты.
Решение:
1 способ решения задачи:
Мы знаем, что энергию плоского конденсатора можно найти по формуле:
\[W=\frac{q^2}{2C}\left(1.1\right),\]где $C$ -- емкость плоского конденсатора.
Основой для решения задачи сделаем уравнение:
\[F_x=-\frac{\partial }{\partial x}{\left(\frac{q^2}{2C}\right)}_q=-\frac{q^2}{2}\frac{\partial }{\partial x}\left(\frac{1}{C}\right)=\frac{q^2}{2C^2}\frac{\partial C}{\partial x}.\]2 способ решения задачи:
Мы знаем, что энергию плоского конденсатора можно найти по формуле:
\[W=\frac{U^2C}{2}\left(1.3\right).\]Основой для решения задачи сделаем уравнение:
\[{F_x}'={\left(\frac{\partial W}{\partial x}\right)}_{\varphi }=\frac{\partial }{\partial x}\left(\frac{U^2C}{2}\right)=\frac{U^2}{2}\frac{\partial C}{\partial x}\ \left(1.4\right).\]Зная, что:
\[q=CU\ \to U=\frac{q}{C}\left(1.5\right).\]Подставим (1.5) в (1.4), получим:
\[{F_x}'=\frac{q^2}{2C}\frac{\partial C}{\partial x}\ \left(1.6\right).\]Мы получили, что ${F_x}'=F_x=\frac{q^2}{2C}\frac{\partial C}{\partial x}$.
Задание: Две проводящие плоские пластины образуют угол $\alpha $. Длина пластин, перпендикулярных плоскости рис. 1 бесконечна. Между пластинами постоянная разность потенциалов равна U. Ширина пластины b-a. Пластины не соприкасаются в точке O. Краевыми эффектами пренебречь. Можно использовать, то, что емкость такого конденсатора равна:$\ C=\frac{l\cdot \varepsilon \cdot ln\left(\frac{b}{a}\right)}{\alpha }$. Найдите момент силы ($M$), который сближает пластины конденсатора используя формулы связи пондемоторных сил с энергией. Сравните результат, который получен во 2-м примере в статье «Пондеромоторные силы в электрическом поле и методы их вычисления».
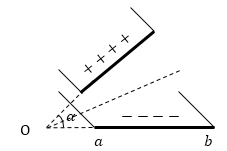
Рис. 1
Решение:
Энергия конденсатора равна:
\[W=\frac{U^2C}{2}\left(2.1\right),\]где в качестве емкости используем выражение:
\[C=\frac{l\cdot \varepsilon \cdot ln\left(\frac{b}{a}\right)}{\alpha }\left(2.2\right).\]Момент сил (М), действующих на пластины в поле относительно оси поворота, которая совпадает с линией пересечения пластин, стремится изменить угол между пластинами, равен:
\[M={\left(\frac{\partial W}{?\alpha }\right)}_{\varphi }=\frac{\partial }{?\alpha }\left(\frac{U^2C}{2}\right)=\frac{U^2}{2}\frac{\partial }{?\alpha }\left(\frac{l\cdot \varepsilon \cdot ln\left(\frac{b}{a}\right)}{2\alpha }\right)=\frac{U^2l\cdot \varepsilon \cdot ln\left(\frac{b}{a}\right)}{2}\frac{\partial }{?\alpha }\left({\alpha }^{-1}\right)=-\frac{U^2l\cdot \varepsilon \cdot ln\left(\frac{b}{a}\right)}{2{\alpha }^2}\left(2.3\right),\]где знак минус означает, что момент сил стремится уменьшить угол между пластинами.
Ответ: $M=-\frac{U^2l\cdot \varepsilon \cdot ln\left(\frac{b}{a}\right)}{2{\alpha }^2}.$ Результат получился такой же, как в разделе «Пондеромоторные силы в электрическом поле и методы их вычисления».











