Принципиальный способ измерений векторов $\overrightarrow{E}\ $и $\overrightarrow{D}$ строят на основе граничных условий для данных векторов при переходе поля через границу двух диэлектриков:
Обычный метод измерения напряженности
Надо сказать, что обычным считается метод измерения напряженности по силе, которая действует на пробный заряд, который помещают в поле. Однако данный метод хорошо применим для поля в вакууме, но не всегда пригоден для поля в веществе. Так как равенство:
справедливо в вакууме, в веществе оно является приближенным. Помимо того, сам процесс внесения пробного заряда в диэлектрик может стать невозможным, к примеру, если диэлектрик твердый. Единственный способ измерения $\overrightarrow{E}\ $и $\overrightarrow{D}$, который и называется принципиальным -- это сделать внутри вещества полость и в нее внести пробный заряд. Надо заметить при этом, что поле, которое измерили таким способом, не будет совпадать ни с вектором напряженности, ни с вектором индукции электрического поля. Результат, конечно, зависит от формы полости. Поэтому для применения такого метода измерения векторов поля подбирают специальные формы полостей, измерение в которых $\overrightarrow{E}\ $и $\overrightarrow{D}$ дают близкие к реальности результаты.
Измерение векторов поля при помощи полостей
Например, делают полость, которая имеет форму длинного и тонкого цилиндрического канала, который параллелен полю $\overrightarrow{E}$ (рис.1). Количество вещества, которое было в канале считают бесконечно малым. Удаление такого количества вещества из диэлектрика немного изменяет электрическое поле в среде. На концах канала появляются поляризационные заряды, но влиянием этих зарядов на поле на достаточном удалении от концов полости, можно пренебречь. Из-за симметрии следует, что поле в канале ($\overrightarrow{E_0}$) параллельно внешнему полю $(\overrightarrow{E)}.$ Из граничного условия (2) следует, что:
В результате получаем, что измерение поля в диэлектрике сводится к измерению поля $\overrightarrow{E_0}$.
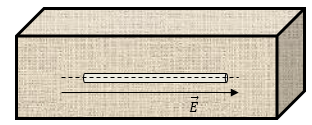
Рис. 1
Другой вариант используемой формы полости. Полость в виде бесконечно короткого цилиндра, основания которой перпендикулярны вектору индукции электрического поля ($\overrightarrow{D}$) (рис.2).
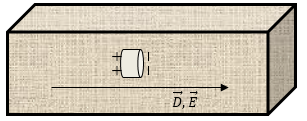
Рис. 2
В данном случае, удаление из диэлектрика вещества не окажет существенного влияния на электрическое поле в диэлектрике в целом. На границах полости возникнут поляризационные заряды противоположных знаков. Вне полости поля этих зарядов практически полностью компенсируют друг друга. Внутри полости поля этих зарядов усиливают друг друга, что заметно изменяет поле внутри полости. Внутри полости $\overrightarrow{E_0}$ из-за симметрии, перпендикулярно к основаниям полости. Так как в полости вакуум или воздух, то:
Используем граничное условие (1), получим:
Так, мы получили, что измерение электрического смещения сведется к измерению напряженности поля в полости.
Задание: В шаре, равномерно заряженном с объемной плотностью $\rho $, сделана маленькая сферическая полость, центр которой $O'$ находится на расстоянии $b$ относительно центра диэлектрического шара $O$. Определите напряженность поля в центре полости.
Решение:
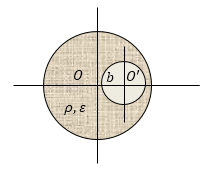
Рис. 3
Для нахождения поля в полости необходимо использовать теорему Остроградского - Гаусса и принцип суперпозиции. Найдем поле шара в точке $O'$. Для этого построим гипотетическую сферу радиуса b с центром в точке O. Найдем поток вектора электрического смещения сквозь поверхность данной сферы:
\[Ф_D=\oint\limits_S{DdS}=q\left(1.1\right),\]где $q=\frac{4}{3}\pi b^3\rho $, $S=4\pi b^2$. Поле шара обладает сферической симметрией, поэтому из (1.1) можно записать:
\[DS=D4\pi b^2=\frac{4}{3}\pi b^3\rho \to D=\frac{b\rho }{3}\left(1.2\right).\]Поляризационные заряды в полости создают поле $\ \overrightarrow{D'}$, и по принципу суперпозиции результирующее поле в точке $O'$ равно:
\[\overrightarrow{D_{o'}}=\overrightarrow{D}+\overrightarrow{D'}\left(1.3\right).\]В полости свободных зарядов нет, следовательно, по теореме Остроградского -- Гаусса:
\[\overrightarrow{D'}=0\ \left(1.4\right).\]Из граничных условий мы знаем, что нормальная составляющая вектора электрического смещения при переходе через границу раздела диэлектриков не изменяется, то есть:
\[D_{1n}=D_{2n}\left(1.5\right).\]Из вышесказанного следует сделать вывод о том, что внутри полости поле равно:
\[D_{O'}=D=\frac{b\rho }{3}.\]Напряженность поля в полости в таком случае будет иметь вид:
\[\overrightarrow{E}=\frac{\overrightarrow{b}\rho }{3{\varepsilon }_0}.\]Ответ: Поле в полости $\overrightarrow{D_{O'}}=\frac{\overrightarrow{b}\rho }{3},\ \overrightarrow{E}=\frac{\overrightarrow{b}\rho }{3{\varepsilon }_0},где\ \overrightarrow{b}$ -- вектор, соединяющий точки $O$ и $O'$.
Задание: Найдите напряженность электрического поля на оси бесконечно длинной цилиндрической полости, которая находится в равномерно заряженном по объему с плотностью заряда ${\mathbf \rho }$ бесконечно длинном цилиндре радиуса $R$. Оси цилиндра и полости параллельны и находятся на расстоянии a друг от друга.
Решение:
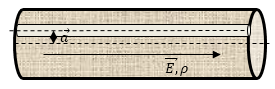
Рис. 4
Для нахождения поля в полости необходимо использовать теорему Остроградского - Гаусса и принцип суперпозиции. Найдем поле цилиндра на прямой, где должна находиться ось полости. Для этого построим гипотетическую цилиндрическую поверхность радиуса a с осью, которая совпадает с осью основного цилиндра. Найдем поток вектора электрического смещения сквозь поверхность данного цилиндра:
\[Ф_E=\oint\limits_S{DdS}=q\left(2.1\right),\]где $q=\pi a^2h\rho $, $S=2\pi ah$ ($h$ - высота цилиндра). Поле шара обладает цилиндрической симметрией, поэтому из (1.1) можно записать:
\[DS=D2\pi ah=\pi a^2h\rho \to D=\frac{a\rho }{2}\left(2.2\right).\]Поляризационные заряды в полости создают поле$\ \overrightarrow{D'}$, и по принципу суперпозиции результирующее поле на оси полости равно:
\[\overrightarrow{D_{o'}}=\overrightarrow{D}+\overrightarrow{D'}\left(2.3\right).\]В полости свободных зарядов нет, следовательно, по теореме Остроградского -- Гаусса:
\[\overrightarrow{D'}=0\ \left(2.4\right).\]Из граничных условий мы знаем, что нормальная составляющая вектора электрического смещения при переходе через границу раздела диэлектриков не изменяется, то есть:
\[D_{1n}=D_{2n}\left(2.5\right).\]Из вышесказанного следует сделать вывод о том, что внутри полости поле равно:
\[D_{O'}=D=\frac{a\rho }{2}.\]Напряженность поля в полости в таком случае будет иметь вид:
\[\overrightarrow{E}=\frac{\overrightarrow{a}\rho }{2{\varepsilon }_0}.\]Ответ: $\overrightarrow{E}=\frac{\overrightarrow{a}\rho }{2{\varepsilon }_0}.$











