
Принцип суперпозиции
Допустим, что у нас есть три точечных заряда. Эти заряды взаимодействуют. Можно провести эксперимент и измерить силы, которые действуют на каждый заряд. Для того чтобы найти суммарную силу, с которой на один заряд действует второй и третий, необходимо силы, с которыми действуют каждый из них сложить по правилу параллелограмма. Возникает вопрос, равна ли измеряемая сила, которая действует на каждый из зарядов, сумме сил со стороны двух других, если силы рассчитаны по закону Кулона. Исследования показали, что измеряемая сила равна сумме вычисляемых сил в соответствии с законом Кулона со стороны двух зарядов. Такой эмпирический результат выражается в виде утверждений:
- сила взаимодействия двух точечных зарядов не изменяется, если присутствуют другие заряды;
- сила, действующая на точечный заряд со стороны двух точечных зарядов, равна сумме сил, действующих на него со стороны каждого из точечных зарядов при отсутствии другого.
Данное утверждение называется принципом суперпозиции. Этот принцип является одной из основ учения об электричестве. Он так же важен, как и закон Кулона. Его обобщение на случай множества зарядов очевидно. Если имеется несколько источников поля (количество зарядов N), то результирующую силу, действующую на пробный заряд q можно найти как:
\[\overrightarrow{F}=\sum\limits^N_{i=1}{\overrightarrow{F_{ia}}}\left(1\right),\]где $\overrightarrow{F_{ia}}$ -- сила, с которой действует на заряд q заряд $q_i$ если остальные N-1 заряд отсутствуют.
Принцип суперпозиции (1) позволяет, используя закон взаимодействия между точечными зарядами, вычислить силу взаимодействия между зарядами, находящимися на теле конечных размеров. Для этого необходимо разбить каждый из зарядов на малые заряды dq, которые можно считать точечными, взять из попарно, вычислить силу взаимодействия и провести векторное сложение полученных сил.
Полевая трактовка принципа суперпозиции
Принцип суперпозиции имеет полевую трактовку: напряженность поля двух точечных зарядов равна сумме напряженностей, которые создаются каждым из зарядов, при отсутствии другого.
В общем случае принцип суперпозиции относительно напряженностей можно записать так:
\[\overrightarrow{E}=\sum{\overrightarrow{E_i}}\left(2\right).\]где ${\overrightarrow{E}}_i=\frac{1}{4\pi {\varepsilon }_0}\frac{q_i}{\varepsilon r^3_i}\overrightarrow{r_i}\ $- напряжённость i-го точечного заряда, $\overrightarrow{r_i}\ $- радиус-вектор, проведённый от i-го заряда в точку пространства. Выражение (1) означает, что напряженность поля любого числа точечных зарядов равна сумме напряженностей полей каждого из точечных зарядов, если другие отсутствуют.
Подтверждено инженерной практикой, что принцип суперпозиции соблюдается вплоть до очень больших напряженностей полей. Очень значительные напряженности имеют поля в атомах и ядрах (порядка ${10}^{11}-{10}^{17}\frac{B}{м}$), но и для них использовали принцип суперпозиции в расчетах энергетических уровней атомов и данные расчетов совпали с данными экспериментов с большой точностью. Однако надо отметить, что при очень малых расстояниях (порядка $\sim {10}^{-15}м$) и экстремально сильных полях принцип суперпозиции, возможно, не выполняется. Так, к примеру, на поверхности тяжелых ядер напряженности достигают порядка $\sim {10}^{22}\frac{В}{м}$ принцип суперпозиции выполняется, но при напряженности ${10}^{20}\frac{В}{м}$ возникают квантово -- механические нелинейности взаимодействия.
Если заряд распределен непрерывно (нет необходимости учитывать дискретность), то суммарная напряженность поля найдется как:
\[\overrightarrow{E}=\int{d\overrightarrow{E}}\ \left(3\right).\]В уравнении (3) интегрирование проводят по области распределения зарядов. Если заряды распределены по линии ($\tau =\frac{dq\ }{dl}-линейная\ плотность\ распределения\ заряда$), то интегрирование в (3) проводят по линии. Если заряды распределены по поверхности и поверхностная плотность распределения $\sigma =\frac{dq\ }{dS}$, то интегрируют по поверхности. Интегрирование проводят по объему, если имеют дело с объемным распределением заряда: $\rho =\frac{dq\ }{dV}$, где $\rho $ -- объемная плотность распределения заряда.
Принцип суперпозиции в принципе позволяет определить $\overrightarrow{E}$ для любой точки пространства по известному пространственному распределению заряда.
Задание: Одинаковые точечные заряды q находятся в вершинах квадрата со стороной a. Определите, какая сила, действует на каждый заряд со стороны других трех зарядов.
Решение:
Изобразим силы, действующие на один из зарядов в вершине квадрата (выбор не важен, так как заряды одинаковы) (рис.1). Результирующую силу, действующую на заряд $q_1$, запишем как:
\[\overrightarrow{F}={\overrightarrow{F}}_{12}+{\overrightarrow{F}}_{14}+{\overrightarrow{F}}_{13}\ \left(1.1\right).\]Силы ${\overrightarrow{F}}_{12}$ и ${\overrightarrow{F}}_{14}$ равны по модулю и могут быть найдены как:
\[\left|{\overrightarrow{F}}_{12}\right|=\left|{\overrightarrow{F}}_{14}\right|=k\frac{q^2}{a^2}\ \left(1.2\right),\]где $k=9•{10}^9\frac{Нм^2}{{Кл}^2}.$
Модуль силы ${\overrightarrow{F}}_{13}$ найдем, также по закону Кулона, зная, что диагональ квадрата равна:
\[d=\sqrt{2}a\ \left(1.3\right),\]следовательно, имеем:
\[\left|{\overrightarrow{F}}_{13}\right|=k\frac{q^2}{2a^2}\ \left(1.4\right)\]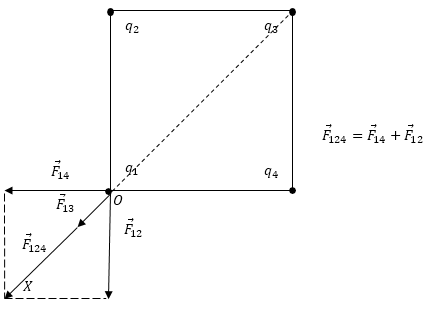
Рис. 1
Направим ось OX как указано на рис. 1, спроектируем уравнение (1.1), подставим полученные модули сил, получим:
\[F=2k\frac{q^2}{a^2}\cdot \frac{\sqrt{2}}{2}+k\frac{q^2}{2a^2}=\frac{kq^2}{a^2}\left(\frac{2\sqrt{2}+1}{2}\right).\]Ответ: Сила, действующая на каждый из зарядов в вершинах квадрата равна: $F=\frac{kq^2}{a^2}\left(\frac{2\sqrt{2}+1}{2}\right).$
Задание: Электрический заряд равномерно распределен вдоль тонкой нити в равномерной линейной плотностью $\tau $. Найдите выражение для напряженности поля на расстоянии $а$ от конца нити на ее продолжении. Длина нити равна $l$.

Рис. 2
Решение:
Выделим на нити точечный заряд $dq$, запишем для него из закона Кулона выражение для напряженности электростатического поля:
\[d\overrightarrow{E}=k\frac{dq}{r^3}\overrightarrow{r\ }\left(2.1\right).\]В заданной точке все векторы напряженности направлены одинаково, вдоль оси Х, поэтому, имеем:
\[dE_x=k\frac{dq}{r^2}=dE\left(2.2\right).\]Так как заряд по условию задачи равномерно распределен по нити с линейной плотностью $\tau $, то можно записать следующее:
\[dq=\tau dr\left(2.4\right).\]Подставим (2.4) в уравнение (2.1), проинтегрируем:
\[E=k\int\limits^{l+a}_a{\frac{\tau dr}{r^2}}=k\tau \left(-{\left.\frac{1}{r}\right|}^{l+a}_a\right)=\frac{k\tau l}{a(l+a)}.\]Ответ: Напряженность поля нити в указанной точке вычисляется по формуле: $E=\frac{k\tau l}{a(l+a)}.$











