При переходе через границу двух различных диэлектриков можно записать следующее выражение:
где $P_{2n}$-нормальная составляющая вектора поляризации диэлектрика с номером 2, $P_{1n}$ - нормальная составляющая вектора поляризации диэлектрика с номером 1. Для определенности будем считать, что ${\varepsilon }_2>{\varepsilon }_1$, а вектор напряженности направлен из первой среды во вторую. В качестве положительной выберем нормаль, которая направлена во вторую среду. Тогда величины $P_{1n},\ P_{2n}$- положительные, а связанный заряд будет отрицательным. Поведение нормальной составляющей вектора поляризации можно изобразить рис.1. Причем из (1) и того, что $у_{sv}
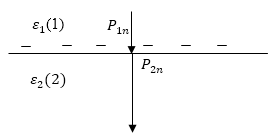
Рис. 1
Напомним, что в изотропном диэлектрике связь между поляризованность и напряженностью для большого класса диэлектриков и широкого круга явлений линейна и однородна, то есть:
где $\varkappa $ -- диэлектрическая восприимчивость (безразмерная величина), уравнение записано в системе СИ. Вектор поляризации направлен в таком случае либо также как вектор $\overrightarrow{E}$ или в противоположном направлении. Следовательно, тангенциальная составляющая вектор поляризованности будет вести себя так же как тангенциальная составляющая вектора напряженности, поведение которой мы рассмотрим чуть дальше.
Закон преломления линий поля на границе двух диэлектриков
Пусть на границе раздела двух диэлектриков нет свободных зарядов. В таком случае мы можем записать, что для нормальной составляющей вектора напряженности ($E_n$) выполняется равенство:
Для тангенциальной составляющей ($E_{\tau }$) мы имеем:
В том случае, если ${\varepsilon }_2>{\varepsilon }_1$, тогда $E_{1n}>E_{2n}$, тогда силовые линии можно изобразить так, как показано на рис. 2.
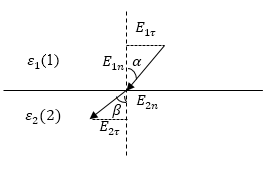
Рис. 2
На рис.2 видно, что силовые линии удаляются от нормали, если переход происходит из диэлектрика с меньшей диэлектрической проницаемостью в диэлектрик с большей диэлектрической проницаемостью. При чем, из того же рисунка очевидно соотношение:
где $\alpha $- угол между нормалью к границе раздела двух диэлектриков и направлением вектора напряженности поля в первой среде. Кроме того, можно записать, что:
где $\beta $- угол между нормалью к среде раздела двух диэлектриков и направлением вектора напряженности во второй среде. Разделим выражение (3) на (4), получим:
Используем соотношения (1) и (2), получим:
Уравнение (8) называют законом преломления линий поля на границе двух диэлектриков.
Закон преломления линий электрического смещения
На границе диэлектриков линии электрического смещения терпят преломление, угол между нормалью к поверхности раздела и линией электрического смещения изменяется ($\alpha \to \beta $). Аналогично, как для вектора напряженности, легко получить:
\[\frac{tg\alpha }{tg\beta }=\frac{D_{1\tau }}{D_{1n}}:\frac{D_{2\tau }}{D_{2n}}\left(9\right).\]А мы знаем, что на границе двух диэлектриков выполняются следующие условия:
\[\frac{D_{2\tau }}{D_{1\tau }}=\frac{{\varepsilon }_2}{{\varepsilon }_1},\ D_{1n}=D_{2n}\left(10\right),\ \]следовательно, подставляя граничные условия для составляющих вектора смещения в (9) получим закон преломления линий электрического смещения:
\[\frac{tg\alpha }{tg\beta }=\frac{D_{1\tau }}{D_{2\tau }}=\frac{{\varepsilon }_1}{{\varepsilon }_2}(11).\]Сравним (11) и (7), можем записать:
\[\frac{E_{2n}}{E_{1n}}=\frac{D_{2\tau }}{D_{1\tau }}=\frac{{\varepsilon }_2}{{\varepsilon }_1}\ \left(12\right).\]Для углов падения и преломления получим:
\[tg\alpha =\frac{E_{1ф}}{E_{1n}}=\frac{D_{1\tau }}{D_{1n}},\ tg\beta =\frac{E_{2\tau }}{E_{2n}}=\frac{D_{2\tau }}{D_{2n}}\left(13\right).\]Задание: На рис. 3 изображена картина линий вектора $\overrightarrow{E}\ $при переходе их одного диэлектрика (${\varepsilon }_1$) в другой (${\varepsilon }_2$). Какая из диэлектрических проницаемостей среды больше?
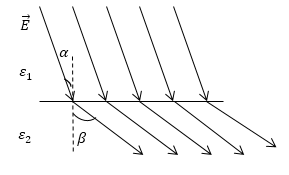
Рис. 3
Решение:
Рассмотрим, как ведут себя силовые линии при прохождении через границу раздела двух диэлектриков. При переходе через границу раздела двух диэлектриков, если отсутствуют свободные заряды выполняется условие:
\[\frac{tg\alpha }{tg\beta }=\frac{E_{2n}}{E_{1n}}=\frac{{\varepsilon }_2}{{\varepsilon }_1}\ \left(1.1\right).\]Это означает, что в диэлектрике с большей диэлектрической проницаемостью, вектор напряженности составляет больший угол с нормалью к границе раздела двух диэлектриков.
Следовательно, в нашей задаче ${\varepsilon }_2>{\varepsilon }_1$.
Ответ: ${\varepsilon }_2>{\varepsilon }_1$.
Задание: Диэлектрическая пластина внесена в однородное электрическое поле (рис.4), изобразите силовые линии поля в области 2, 3. Учесть, что ${\varepsilon }_1
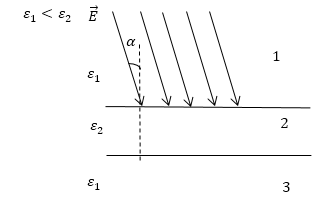
Рис. 4
Решение:
При переходе из диэлектрика с меньшей плотностью (${\varepsilon }_1)$ в диэлектрик с большей плотностью(${\varepsilon }_2$) силовые линии поля отклоняются от нормали к границе раздела диэлектриков на больший угол ($\alpha
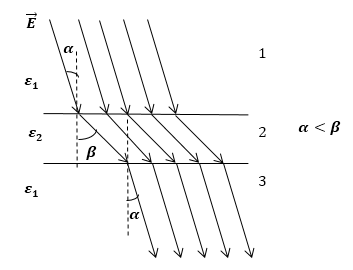
Рис. 5












