Основной величиной, с помощью которой характеризуют электрическое поле, является напряженность ($\overrightarrow{E}$). Ее можно вычислить как:
где $\overrightarrow{F}$- механическая (пондемоторная сила), которая действует в данной точке поля на пробный заряд $q$. При этом надо помнить, что поле создается всеми зарядами системы кроме самого заряда $q$.
Результирующая сила
Более сложным является вопрос о механических силах, которые действуют на поверхностные заряды, поскольку напряженность поля имеет по обе стороны поверхности, которая несет заряд, разные направления и поэтому на самой поверхности является неопределённой.
Если мы имеем уединенный заряженный проводник, то взаимно отталкивающиеся элементы заряда проводника покинуть его поверхность не могут и в результате к поверхности проводника приложены пондемоторные силы, которые стремятся его растянуть. Подобные силы будут действовать и на неодиночные проводники в электрическом поле. На элементарный заряд $dq$, который находится на элементе поверхности $dS$, действует половина напряженности поля, которое имеет проводник, так как вторая половина создается самим рассматриваемым зарядом элемента поверхности. Таким образом, поверхностная плотность такой силы равна:
где $\sigma $ -- поверхностная плотность заряда проводника, $\overrightarrow{n\ }$ - единичный вектор внешней нормали к поверхности проводника, $\varepsilon $ -- диэлектрическая проницаемость среды с которой граничит проводник. И так, на поверхности заряженного проводника сила действует в направлении внешней нормали, стремясь увеличить объем тела. Соответственно, результирующая сила может быть найдена как:
где $S$ -- поверхность проводника.
Объёмные силы
В диэлектрике объёмные электростатические силы в состоянии равновесия не вызывают движения элементов объема, но пытаются деформировать среду. В результате возникают объемные силы упругости, которые уравновешивают электростатические силы. Объемные электрические силы вызывают движения элементарных объемов только при быстром изменении полей. Для изотропных сжимаемых диэлектриков с любой зависимостью $\varepsilon \ $от плотности массы (${\rho }_m$) объемна плотность пондемоторной силы ($\overrightarrow{f}$) действующей в диэлектрике, который помещен в электрическое поле равна:
Если поляризованность линейна по отношению к ${\rho }_m$, то:
Поверхностные пондемоторные силы
Помимо объёмных сил в диэлектриках действуют и поверхностные пондемоторные силы.
Рассмотрим плоскую границу диэлектриков, параллельную обкладкам конденсатора. При этом напряженность поля, которое можно считать однородным, перпендикулярна границе диэлектриков. Положительной нормалью выберем нормаль, которая направлена из первой среды во вторую. При этом поверхностная плотность силы имеет вид:
где $E_{n,\ }D_n=D_{2n}$=$D_{1n}$ -- нормальные составляющие векторов напряженности и электрической индукции.$\ {\varepsilon }_1$, ${\varepsilon }_2$ -- диэлектрические проницаемости диэлектриков. Из уравнения (4) очевидно, что при ${\varepsilon }_1>{\varepsilon }_2\to f>0.$ На границу раздела диэлектриков сила действует в сторону диэлектрика с меньшей диэлектрической проницаемостью.
Поверхностная плотность силы
Поверхностная плотность силы складывается из двух частей:
- поверхностной плотности силы ($f_2$), действующей на границу раздела диэлектриков, направленную в первую среду со стороны электрического поля второй среды, которая определяется как: \[f_2=\frac{1}{2}E_{2n}D_{2n}\left(7\right),\]
- плотности силы, действующей на границу против направления положительной нормали со стороны электрического поля первой среды ($f_1$): \[f_1=-\frac{1}{2}E_{1n}D_{1n}\left(8\right).\]
где сила направлена по положительной нормали, которая условно направлена из первой среды во вторую;
В таком случае, электрические поля, которые находятся по разные стороны границы диэлектриков, «притягивают» поверхность раздела с поверхностной плотностью силы, равной объемной плотности электрической энергии, которая приходится на нормальные составляющие векторов поля.
Рассмотрим диэлектрики, плоская граница между которыми перпендикулярна обкладкам плоского конденсатора.
Эта поверхностная плотность силы складывается из двух частей:
- поверхностной плотности силы ($f_2$), действующей на границу раздела диэлектриков, направленную в первую среду со стороны электрического поля второй среды, которая определяется как: \[f_2=-\frac{1}{2}E_{2\tau }D_{2\tau }\left(9\right),\]
- плотности силы, действующей на границу в направлении положительной нормали со стороны электрического поля первой среды ($f_1$): \[f_1=\frac{1}{2}E_{1\tau }D_{1\tau }\left(10\right).\]
где знак минус указывает, что сила направлена против положительной нормали, которая условно направлена из первой среды во вторую;
Получается, что электрическое поле «давит» на границу раздела за счет тангенциальной составляющей поля. Так как $E_{1\tau }$=$E_{2\tau }=E_\tau$, то равнодействующая сил давления равна:
\[f=\frac{1}{2}E^2_{\tau }\left({\varepsilon }_1-{\varepsilon }_2\right)\left(11\right).\]Пондемоторные силы часто вычисляют, используя связь между энергией электрического поля и силами, которые действуют на тела, находящиеся в этом поле. О таком методе расчета рассказано в статье: «Связь пондеромоторных сил с энергией электрических зарядов».
Задание: Получите зависимость пондемоторной силы, действующей на диполь в произвольном электрическом поле, напряженность которого определяется вектором $\overrightarrow{E\ },\ $может изменяться в пространстве. Заряды диполя по модулю равны $q, l$ -- плечо диполя.
Решение:
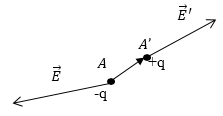
Рис. 1
Пусть $\overrightarrow{E}\ и\ \overrightarrow{E}'$ - напряженности поля в точках $A\ и\ A'$в которое помещен диполь (рис.1). Найдем равнодействующую силу ($\overrightarrow{F}$), действующую на диполь:
\[\overrightarrow{F}=q{\overrightarrow{E}}'-q\overrightarrow{E}=q\left({\overrightarrow{E}}'-\overrightarrow{E}\right)\left(1.1\right),\]где ${(\overrightarrow{E}}'-\overrightarrow{E})$ -- приращение вектора напряженности на отрезке $A\ \ A'$, который равен длине диполя (l). Так как l мало, то можно записать, что:
\[{\overrightarrow{E}}'-\overrightarrow{E}=l\frac{\partial \overrightarrow{E}}{\partial l}=\overrightarrow{l}\nabla \overrightarrow{E\ }\left(1.2\right).\]Подставим (1.2) в (1.1), получим:
\[\overrightarrow{F}=q\overrightarrow{l}\nabla \overrightarrow{E\ }.\]Ответ: Пондемоторная сила, действующая на диполь в электрическом поле, зависит от скорости изменения этого поля в направлении оси диполя: $\overrightarrow{F}=q\overrightarrow{l}\nabla \overrightarrow{E\ }$.
Задание: Две проводящие плоские пластины образуют угол $\alpha $. Длина пластин, перпендикулярных плоскости рис.2 бесконечна. Между пластинами постоянная разность потенциалов равна U. Ширина пластины b-a. Пластины не соприкасаются в точке O. Краевыми эффектами пренебречь. Можно использовать, то, что поверхностная плотность заряда пластин такого конденсатора равна:$\ \sigma =\frac{\varepsilon U}{r\alpha }$,где r -- расстояние от оси. Найдите момент силы ($M$), который сближает пластины конденсатора.
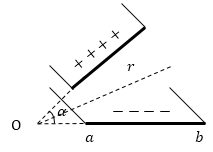
Рис. 2
Решение:
Поверхностная плотность силы, которая действует на проводник, равна:
\[f=\frac{{\sigma }^2}{2\varepsilon }\ \left(2.1\right).\]Следовательно, на слой длиной $l$ между $r$ и $r+dr$ действует сила равная:
\[dF=-fldr=-\frac{\varepsilon U^2}{2{\alpha }^2r^2}l\ dr\left(2.2\right),\]где $\sigma =\frac{\varepsilon U}{r\alpha }$. Знак минус учитывает, что сила стремится уменьшить угол между пластинами. Найдем результирующую силу $(F):$
\[F=\int\limits^b_a{dF}=-\frac{\varepsilon U^2l}{2{\alpha }^2}\int\limits^b_a{\frac{dr}{r^2}}=\frac{\varepsilon U^2l}{2{\alpha }^2}\left(\frac{1}{b}-\frac{1}{a}\right)=\frac{\varepsilon U^2l}{2{\alpha }^2}\cdot \frac{a-b}{ab}\left(2.3\right).\]Линия приложения сил находится на расстоянии $r_0\ от\ $оси вращения. Это расстояние найдем из условия:
\[r_0F=\int\limits^b_a{rdF=-}\frac{\varepsilon U^2l}{2{\alpha }^2}ln\left(\frac{b}{a}\right)\to r_0=\frac{ab}{a-b}ln\left(\frac{b}{a}\right)\ \left(2.4\right).\]В таком случае, момент силы относительно оси вращения равен:
\[M=r_0F=-\frac{\varepsilon U^2l}{2{\alpha }^2}ln\left(\frac{b}{a}\right).\]Ответ: $M=-\frac{\varepsilon U^2l}{2{\alpha }^2}ln\left(\frac{b}{a}\right).$











