Что такое метод изображений
Метод изображений - наглядный метод построения электрического поля. Суть его заключена в следующем. Так как поле точечного заряда тщательно исследовано, то стараются подобрать такую совокупность точечных зарядов, результирующее поле которых удовлетворяет условиям задачи.
Теорема о единственности решения при этом говорит о том, что такое поле дает решение, которое искали. С точки зрения математики задача заключается в нахождении потенциала, который удовлетворит условиям задачи. Напряженность же поля находят из соотношения:
\[\overrightarrow{E}=-grad\varphi \ \left(1\right).\]При чем известно, что вектор напряженности направлен перпендикулярно эквипотенциальным поверхностям. Получить форму эквипотенциальных поверхностей системы точечных зарядов не так сложно.
Форма эквипотенциальных поверхностей
Пусть мы имеем несколько точечных зарядов. При этом $S$ - эквипотенциальная поверхность, которая делит пространство на два полупространства (1) и (2). В полупространстве (1) заряды обозначим как $q_1,\ q_2,\ \dots ,$ в полупространстве (2) заряды будут: ${q'}_1,\ {q'}_2,\ \dots .$ Если заданы величины зарядов и их расположения, потенциал поверхности $S$, тогда поле в полупространстве определено однозначно (согласно теореме о единственности). Это относится и к полупространству (1), и к полупространству (2). В том случае если поверхность $S$ является проводящей, то поле во всем пространстве ни как не изменится. Но при этом поля в полупространствах при этом совершенно независимы друг от друга.
Так решаются одновременно две аналогичные задачи. Одна из них: В полупространстве (1) находятся точечные заряды $q_1,\ q_2,\ \dots .\ $Необходимо найти электрическое поле (вектор напряженности) в этом полупространстве. Это поле складывается из полей отдельных зарядов $q_1,\ q_2,\ \dots ,$ и индуцированных зарядов на поверхности $S$. Но, следуя теореме о единственности, в полупространстве (1) поле индуцированных зарядов такое же, как поле зарядов ${q'}_1,\ {q'}_2,\ \dots .$ Следовательно, при вычислении напряженности искомого поля поверхность S можно удалить и заменить ее точечными зарядами ${q'}_1,\ {q'}_2,\ \dots .$ Система зарядов ${q'}_1,\ {q'}_2,\ \dots .$ при этом называется электрическим изображением зарядов $q_1,\ q_2,\ \dots $ в поверхности $S$. Получается, что задача о поле зарядов, которые находятся по одну сторону проводящей поверхности, ведет к поиску электрических изображений этих зарядов в поверхности S.
Задание: Точечный заряд q находится на расстоянии a от бесконечной проводящей плоскости. Найти силу взаимодействия этого заряда с плоскостью.
Решение:
Заряд ($q'$) равный по величине, имеющий противоположный знак будет электрическим изображением в плоскости $S$, заряда $q$ из условий задачи. То есть $q'=-q$. $q'$ расположен по другую сторону от плоскости $S$ на таком же расстоянии равном а (рис.1). Выберем некоторую точку A.
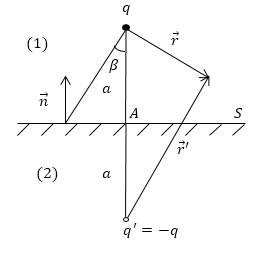
Рис. 1
Для этой точки потенциал поля будет равен:
\[\varphi =kq\left(\frac{1}{r}-\frac{1}{r'}\right)\left(1.1\right),\]где $k=\frac{1}{4\pi {\varepsilon }_0}.$ $\varepsilon =1.$ Потенциал $\varphi $=0 на плоскости $S$. Плоскость $S$ является эквипотенциальной. Формула (1.1) определяет потенциал поля в полупространстве (1). В полупространстве (2), которое заполнено средой, поле равно нулю. Заряд $q$ индуцирует на плоскости $S$ такие заряды, которые создают в полупространстве (1) такое же поле как создавал бы заряд $q'.$ Индуцированные заряды притягивают заряд $q$ с силой равной силе притяжения, которая действует между зарядами $q\ и\ q'$:
\[F=k\frac{q^2}{{(2a)}^2}\ \left(1.2\right),\]где силу $F$ называют силой электрического изображения. В полупространстве (2) индуцированные заряды компенсируют поле заряда $q$.
Ответ: Сила взаимодействия равна $F=k\frac{q^2}{{(2a)}^2}.$
Задание: Найдите силу взаимодействия, которая возникает между точечным зарядом q и проводящим сплошным шаром радиуса R, если точечный заряд находится на расстоянии l от центра сферы считать, что шар заземлен. Найдите энергию взаимодействия того же точечного заряда с тем же шаром, если шар изолирован.
Решение:
Заряд $q$ индуцирует в проводящем шаре свое изображение ($q'$). Потенциал поля, которое создают два точечных заряда равен:
\[\varphi =k\left(\frac{q}{r}-\frac{q'}{r'}\right)\left(2.1\right),\]$\varphi (R)=0$ на поверхности шара потенциал равен нулю. Центр шара лежит на прямой, которая соединяет заряды $q\ и\ q'$. k=$\frac{1}{4\pi {\varepsilon }_0}\varepsilon =1.$
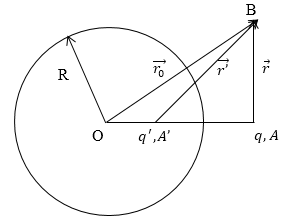
Рис. 2
Расстояние от точки О до точки А равно l, расстояние от точки О до точки $A'$ равно $l'$. При этом выполняются равенства:
\[\frac{l}{l'}={\left(\frac{q}{q'}\right)}^2,\ R^2=ll'\left(2.2\right).\]- Пусть шар заземлен ($\varphi =0$). В таком случае поле за пределами шара, которое создает заряд $q,$ находящийся в точке А (рис.2) будет таким же как поле, которое создают два заряда: заряд $q$ и заряд $-q',\ который\ находится\ в\ точке\ A'$. В данном случае выполняются равенства: \[l'=\frac{R^2}{l},\ q'=\frac{qR}{l}\left(2.3\right).\]
- Допустим, что шар не заряжен и изолирован (это значит, что его заряд поддерживается равным нулю). Для того чтобы полный индуцированный заряд на поверхности проводящего шара был равен нулю следует ввести еще один фиктивный заряд. Он должен быть таким, что полный индуцированный заряд поверхности шара стал равен нулю. И при этом должно сохраниться постоянство потенциала на поверхности шара. Потенциал поля при этом будет выражен следующим образом: \[\varphi =k\left(\frac{q}{r}-\frac{q'}{r'}+\frac{q'}{r_0}\right)\left(2.6\right).\]
Потенциал такого поля равен:
\[\varphi =k\left(\frac{q}{r}-\frac{qR}{lr'}\right)\left(2.4\right).\]На поверхности шара индуцируется заряд не равный нулю. Он равен -$q'.$ Энергия взаимодействия заряда и шара равна:
\[W=-k\frac{qq'}{2\left(l-l'\right)}=-k\frac{q^2R}{2\left(l^2-R^2\right)}\ \left(2.5\right).\]Тогда сила притяжения заряда к шару равна:
\[F=-\frac{\partial W}{\partial l}=-k\frac{q^2lR}{{\left(l^2-R^2\right)}^2}.\]Энергия взаимодействия в таком случае будет записана как:
\[W=-k\frac{qq'}{2}\left(\frac{1}{l}-\frac{1}{l-l'}\right)=-k\frac{q^2R^3}{2l^2\left(l^2-R^2\right)}\ \left(2.7\right).\]Ответ: Сила взаимодействия для случая 1 равна $F=-k\frac{q^2lR}{{\left(l^2-R^2\right)}^2}.$ Энергия взаимодействия для второго случая $W=-k\frac{q^2R^3}{2l^2\left(l^2-R^2\right)}.$











