Локальное поле

Задание: Для модели Лоренца локального поля получите напряжённость поля, которое создают поверхностные заряды сферы ($\overrightarrow{E_1}$).

Решение:

Так как выделенная сфера в модели Лоренца мала, то будем считать, что мы ищем напряженность в ее центре. Напряженность в центре сферы создается связанными зарядами на ее поверхности, как на границе раздела между средой с диэлектрической проницаемостью $\varepsilon \ $и вакуумом (${\varepsilon }_{vak}=1$). Поверхностная плотность связанных (${\sigma }_{sv}$) зарядов равна:

\[{\sigma }_{sv}=-P_{2n\ }\left(1.1\right),\]

где $P_{2n\ }$ - нормальная компонента вектора поляризованности с внешней стороны сферы. Направим ось Z вдоль вектора $\overrightarrow{P}$ (рис.1), получим:

\[{\sigma }_{sv}=-P_{2n}=-Pcos\theta \left(1.2\right).\]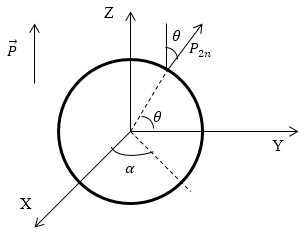

Рис. 1

В телесном угле $d\Omega $ находится заряд ($dq$) равный:

\[dq={\sigma }_{sv}R^2d\Omega \left(1.3\right),\]

где $R$ -- радиус сферы. Этот заряд создает поле в центре сферы с напряжённостью $dE_z$. В направлении оси Z величина $dE_z$ равна:

\[dE_z=-\frac{1}{4\pi {\varepsilon }_0}\frac{dq}{R^2}cos\theta \ \left(1.4\right).\]

Компоненты поля $dE_x=dE_y=0.$ Найдем $E_z$, взяв интеграл от выражения (1.4) и используя (1.3) и (1.2), получим:

\[E_z=E_1=-\frac{1}{4\pi {\varepsilon }_0}\int{\frac{dq}{R^2}cos\theta =-\frac{1}{4\pi {\varepsilon }_0}\int{\frac{{\sigma }_{sv}R^2d\Omega }{R^2}cos\theta =}}\frac{1}{4\pi {\varepsilon }_0}\int{\frac{Pcos\theta R^2d\Omega }{R^2}cos\theta =}\frac{P}{4\pi {\varepsilon }_0}\int{{cos}^2\theta }d\Omega =\int\limits^{2\pi }_0{d\alpha }\int\limits^{\pi }_0{{cos}^2\theta }sin\theta d\theta =\frac{P}{3{\varepsilon }_0}\ \left(1.5\right).\]

В векторной форме напряженность будет иметь вид:

\[\overrightarrow{E_1}=\frac{\overrightarrow{P}}{3{\varepsilon }_0}.\]

Данная формула справедлива только для бесконечного однородного диэлектрика. Если диэлектрик конечен, то напряженность в нем зависит от его размера и формы.

Ответ: $\overrightarrow{E_1}=\frac{\overrightarrow{P}}{3{\varepsilon }_0}.$

В теоретической части в модели Лоренца мы из внутренности сферы удалили вещество и предположили, что $\overrightarrow{E_2}=0.$ Вообще говоря, данное поле зависит от распределения дипольных моментов молекул внутри выделенной сферы и не может быть описано универсальной формулой.

Задание: Вычислите напряженность $\overrightarrow{E_2}$ модели Лоренца для случая, когда молекулы расположены в узлах кубической кристаллической решетки, все дипольные моменты имеют одинаковые направления в пространстве. Такое условие выполняется для индуцированных дипольных моментов.

Решение:

Для определённости будем искать напряженность в узле кристаллической решетки. Поместим начало координат в узел кристаллической решетки, оси X,Y,Z направим по ребрам решетки. Используем в качестве основания для решения формулу напряженности поля диполя:

\[\overrightarrow{E}=\frac{1}{4\pi {\varepsilon }_0}\left[\frac{3\left(\overrightarrow{p}\overrightarrow{r}\right)\overrightarrow{r}}{r^5}-\frac{\overrightarrow{p}}{r^3}\right]\left(2.1\right),\]

где $\overrightarrow{p}$ -- момент диполя $\overrightarrow{r}$ -- радиус-вектор, определяющий местоположение диполя. Формулу (2.1) запишем для проекции вектора напряженности на ось X ($E_{2x}$):

\[E_{2x}=\frac{p_x}{4\pi {\varepsilon }_0}\sum\limits_i{\frac{-r^2_i+3x^2_i}{r^5_i}}+\frac{p_y}{4\pi {\varepsilon }_0}\sum\limits_i{\frac{3x_iy_i}{r^5_i}}+\frac{p_z}{4\pi {\varepsilon }_0}\sum\limits_i{\frac{3x_iz_i}{r^5_i}}\left(2.2\right),\]

где суммирование проводится по всем молекулам малого объема внутренности сферы. Аналогичные формулы можно записать для компонент $E_{2y}$, $E_{2z}$. В формуле (2.2) вычислим сумму по всем молекулам, который находится в малом сферическом слое радиуса r. Из-за кубической симметрии имеем:

\[\sum\limits_i{x^2_i=}\sum\limits_i{y^2_i=\sum\limits_i{z^2_i=\frac{1}{3}}}\sum\limits_i{r^2_i,\ \ \ \sum\limits_i{x_iy_i=\sum\limits_i{y_iz_i=}\sum\limits_i{x_iz_i=0}}}\ \left(2.3\right).\]

В таком случае уравнение (2.2) с учетом (2.3) принимает вид:

\[E_{2x}=\frac{p_x}{4\pi {\varepsilon }_0}\sum\limits_i{\frac{-r^2_i+3x^2_i}{r^5_i}}=\frac{p_x}{4\pi {\varepsilon }_0}\left(-\sum\limits_i{\frac{r^2_i}{r^5_i}}+\frac{1}{3}\sum\limits_i{\frac{3x^2_i}{r^5_i}}\right)=\frac{p_x}{4\pi {\varepsilon }_0}\left(-\sum\limits_i{\frac{1}{r^3_i}}+\sum\limits_i{\frac{1}{r^3_i}}\right)=0\left(2.4\right).\]

Аналогично получится для $E_{2y}=E_{2z}=0.$ То есть окончательно получим: $E_2=0.\ $

Ответ: Получено, что $E_2=0.$