Что такое диэлектрический гистерезис
У сегнетоэлектриков можно наблюдать диэлектрический гистерезис -- неоднозначную зависимость поляризованности ($\overrightarrow{P}$) от напряженности внешнего поля ($\overrightarrow{E}$) при его циклическом изменении.
Так как сегнетоэлектрик обладает доменной структурой, дипольный момент кристалла сегнетоэлектрика в отсутствии диэлектрика равен нулю, вследствие взаимной компенсации дипольных моментов отдельных доменов. В целом, получается, что домен не поляризован. При наложении поля происходит частичное изменение ориентации доменов и увеличение одних доменов, уменьшение других. Это приводит к возникновению в кристалле поляризации ($\overrightarrow{P}$). Зависимость поляризации от напряженности поля представляет рис.1.
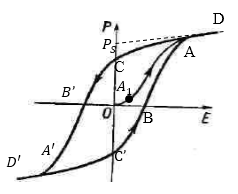
Рис. 1
Сначала рост поляризации идет вдоль кривой ОА. В точке $А$ векторы поляризации всех доменов оказываются ориентированными параллельно полю $\overrightarrow{E}$. Начиная с этой точки рост поляризации идет за счет индуцированной поляризации $\overrightarrow{P_i}\sim \overrightarrow{E}$, линия ОА переходит в участок AD (прямолинейный). При продолжении этого участка до пересечения с осью ординат, он отсечет на ней отрезок, его длина равна спонтанной поляризации $P_S$.
При уменьшении напряженности электрического поля, уменьшение поляризации пойдет не по той же кривой в обратную сторону, а по новой кривой $DAB'A'D'$, которая расположена выше. Это и есть диэлектрический гистерезис сегнетоэлектрика. Процесс изменение ориентации и увеличение доменов в электрическом поле задерживается. Получается, что $\overrightarrow{P}$ не однозначно определен полем $\overrightarrow{E}$, а зависит от «истории» сегнетоэлектрика. Если изменять поле в обратном порядке, то зависимость поляризации от напряженности будет изображена нижней кривой $D'A'BAD$, симметричной с кривой $D'A'B'AD$ относительно начала координат О. Так, получается замкнутая кривая $AB'A'BA$, которая носит название диэлектрической петли гистерезиса. Аналогично можно получить петли для электрической индукции. Если по оси ординат откладывать электрическое смещение ($\overrightarrow{D}$):
\[\overrightarrow{D}={\varepsilon }_0\overrightarrow{E}+\overrightarrow{P}\left(1\right).\ \]Петля гистерезиса для индукции отличается только масштабом от кривых $P=P(E)$, так как в сегнетоэлектриках $E\ll D$, то первым слагаемым в (1) можно пренебречь.
Стрелки на кривой (рис.1) показывают направление движения точки по кривой при изменении напряженности поля. Отрезок ОС характеризует остаточную поляризованность, то есть ту, которую образец сегнетоэлектрика имеет тогда, когда напряженность поля обратилась в ноль. Отрезок $OB'$ характеризует напряженность, имеющую противоположное поляризованности направление, при котором данный сегнетоэлектрик полностью теряет свою поляризацию. Чем больше величина отрезка ОС, тем значительнее остаточная поляризация сегнетоэлектрика. Чем больше размер $OB'$, тем лучше остаточная поляризация удерживается сегнетоэлектриком.
Петля гистерезиса
Петлю гистерезиса легко получить на экране осциллографа. С этой целью соединяют последовательно два конденсатора, пространство между обкладками одного из них заполнено сегнетоэлектриком (его емкость назовем $C_s$). Для питания используют переменный ток от генератора. Так как конденсаторы соединены последовательно, то заряды на их обкладках равны и одинаковы индукции:
\[D_0=D\ \left(2\right),\]где $D_0$ -- индукция поля в конденсаторе с обычным диэлектриком, $D$ - индукция поля в конденсаторе с сегнетоэлектриком. Так как для обычного конденсатора диэлектрическая проницаемость постоянна, то напряжение на обычном конденсаторе пропорционально индукции. Если подать на горизонтально отклоняющие пластины осциллографа напряжение с конденсатора с сегнетоэлектриком, а на вертикально отклоняющие пластины -- с обычного конденсатора, то на экране осциллографа будет воспроизведена петля гистерезиса.
Задание: Объясните, почему говорят, что явление гистерезиса позволяет иллюстрировать роль доменов в поляризации сегнетоэлектрика?
Решение:
Существование доменов в сегнетоэлектрике обуславливает его нелинейные свойства. В первую очередь это нелинейная зависимость поляризации ($\overrightarrow{P}$) от напряженности внешнего поля ($\overrightarrow{E}$):
\[\overrightarrow{P}={\varkappa \left(\overrightarrow{E}\right)\varepsilon }_0\overrightarrow{E}\left(1.1\right),\]где $\varkappa \left(\overrightarrow{E}\right)$ -- диэлектрическая восприимчивость зависит от напряженности внешнего поля. Именно нелинейная зависимость поляризации от внешнего поля приводит в электрических полях к гистерезису.
Рассмотрим подробнее рис. 1. В небольших полях (отрезок $OA_1$) поляризация еще линейно зависит от напряженности, домены к поляризации еще не подключились. На участке $A_1A$ идет интенсивный рост поляризации при увеличении напряженности поля, что связано с нелинейным процессом переориентации доменов вдоль направления внешнего поля. В точке А все домены ориентированы по полю. Дальнейшее возрастание поляризации при росте напряженности внешнего поля идет линейно и оно не связано с доменной структурой. Оно идет за счет индуцированной полем поляризации. Уменьшение напряженности поля начиная от точки А повторяет в обратном порядке процесс первичной поляризации. Наличие остаточной поляризации говорит о том, что сегнетоэлектрик пытается сохранить ориентацию доменов в одном направлении. Приложение поля с обратным направлением ведет к уменьшению поляризации сегнетоэлектрика вплоть до нуля. При дальнейшем повышении напряженности обратного поля происходит переполяризация доменов (изменение знака) и в дальнейшем насыщению (участок $A'D'$), то есть ориентации всех доменов по полю, но в противоположном с участком AD направлении.
Задание: Объясните, почему явление гистерезиса можно наблюдать в ходе опыта, который проводят, используя схему с осциллографом, которая представлена на рис.2. Между обкладками одного плоского конденсатора сегнетоэлектрик, его емкость $C_S$. Пространство между обкладками второго конденсатора (С) заполнено обычным диэлектриком. Питается схема от генератора, который создает гармонически изменяющуюся разность потенциалов на обкладках конденсаторов. Площади обкладок конденсаторов равны, расстояния между обкладками конденсаторов, также равны.
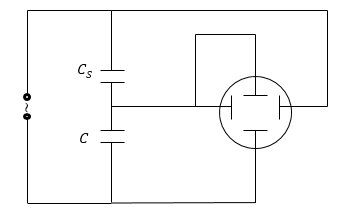
Рис. 2
Решение:
Разность потенциалов распределяется между конденсатором, который содержит сегнетоэлектрик ($С_S$) и воздушным конденсатором $C$. Площади обкладок конденсаторов равны, расстояния между обкладками равно $d$. В таком случае напряженности полей в конденсаторах равны:
\[E=\frac{\sigma }{{\varepsilon }_1{\varepsilon }_0}\left(2.1\right)\ и\] \[E_S=\frac{{\sigma }_S}{{{\varepsilon }_S\varepsilon }_0}\left(2.2\right),\]где $\sigma ,\ {\sigma }_S$- поверхностные плотности распределения зарядов на обкладках конденсаторов, ${\varepsilon }_1$- диэлектрическая проницаемость обычного диэлектрика, ${\varepsilon }_S$ -- диэлектрическая проницаемость сегнетоэлектрика.
Мы знаем, что у последовательно соединенных конденсаторов заряды на обкладках будут равны, а так как у этих конденсаторов одинаковы их геометрические параметры, то можно записать, что:
\[\sigma =\ {\sigma }_S\left(2.3\right).\]Следовательно, разности потенциалов между обкладками:
\[U=Ed=\frac{\sigma d}{{{\varepsilon }_1\varepsilon }_0}\left(2.4\right)\ и\ \] \[U_S=E_Sd=\frac{\sigma d}{{\varepsilon }_S{\varepsilon }_0}\left(2.5\right).\]Найдем отношение $\frac{U_S}{U}$, получим:
\[\frac{U_S}{U}=\frac{уd}{\varepsilon_S \varepsilon_0}:\frac{уd}{{\varepsilon_1 \varepsilon}_0}=\frac{\varepsilon_1}{\varepsilon_S}\ \left(2.6\right).\]Если напряжение U подать на горизонтальную развертку осциллографа, а $U_S$ -- на вертикальную, то можно записать, что:
\[tg\varphi =\frac{U_S}{U}=\frac{{\varepsilon }_1{\varepsilon }_0E}{{\varepsilon }_S{\varepsilon }_0E}\left(2.7\right).\]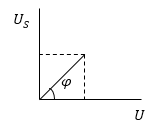
Рис. 3
Таким образом, при изменении напряженности $(E)$, на экране осциллографа будет прочерчена кривая, абсцисса точек которой в определенном масштабе ${\varepsilon }_SE$, а ордината ${\varepsilon }_0{\varepsilon }_1E=D$ в том же масштабе. Получается, что на экране осциллографа вычерчивается кривая гистерезиса.












