Электроемкость проводника
Допустим, мы погрузили проводник в неподвижный диэлектрик. Потенциал проводника будем считать нормированным на бесконечность ($\varphi \left(\infty \right)=0$). Если мы увеличим заряд проводника, то его потенциал увеличится пропорционально. Следовательно, можно записать, что:
где C - электроемкость (или просто емкостью) проводника. Из уравнения (1) следует, что:
В соответствии с выражением (2) емкость равна заряду, который повышает его потенциал на 1 вольт.
Емкость уединенного проводящего шара, радиус которого равен R, находящегося в диэлектрике с проницаемостью $\varepsilon ,\ $ равна:
Единицей емкости является 1 Ф (фарад) -- это емкость проводника, у которого при изменении его заряда на 1 Кл, потенциал изменяется на 1 В. В системе СГС формула (3) для уединенного шара в диэлектрике имеет вид:
\[C=\varepsilon R\ \left(4\right).\]Из (4) следует, что в гауссовой системе единицы емкости совпадают с единицами длины (сантиметрами). $1Ф=9\cdot {10}^{11}см.$ Получается, что емкостью 1Ф обладает шар радиусом $9\cdot {10}^9м$. Для сравнения радиус Земли около R=6,4$\cdot {10}^6м$.
Итак, мы видим, что уединенные проводники имеют небольшую емкость. На практике существует необходимость устройств, которые при небольшом потенциале накапливали бы на себе большие заряды. Такие устройства называют конденсаторами. Основой конденсаторов является то, что емкость проводников увеличивается в случае приближении к нему других тел. Так как под действием поля, которое создается проводником, имеющим заряд в теле, которое подносится к проводнику, возникают индуцированные заряды (на проводнике) или связанные заряды (на диэлектрике). Заряды, которые противоположны по знаку заряду проводника, находятся ближе к проводнику, чем одноименные, они больше влияют на его потенциал. Следовательно, когда к проводнику приближают тело, потенциал проводника уменьшается, а емкость обратно пропорциональная потенциалу возрастает.
Что такое конденсаторы
Конденсаторы - два проводника, которые расположены на маленьком расстоянии друг от друга. При этом проводники конденсатора называют обкладками. Обкладкам конденсаторов придают форму такую, чтобы внешние тела оказывали минимальное влияние на поле, которое создается зарядами, которые накапливает конденсатор. Например, такому требованию соответствует конденсатор в виде двух плоскопараллельных пластин, расположенных на небольшом расстоянии друг от друга. По форме обкладок конденсаторы разделяют на плоские, цилиндрические и сферические конденсаторы. Поле локализуется внутри конденсатора, при этом линии электростатического поля берут начало на одной обкладке и заканчиваются на другой. Сторонние заряды, которые возникают на обкладках конденсатора, имеют одинаковую величину и противоположные по знаки.
Конденсаторы характеризуются своей емкостью, которую определяют как:
\[C=\frac{q}{{\varphi }_1-{\varphi }_2}=\frac{q}{U}\left(5\right),\] где ${\varphi }_1-{\varphi }_2=U$ -- разность потенциалов между обкладками, которую называют напряжением и обозначают U.Емкость зависит от формы конденсатора, размера обкладок, расстояния между ними, также от диэлектрических свойств среды, которая находится в пространстве между обкладками конденсаторов. К примеру, емкость плоского конденсатора вычисляется по формуле:
\[С=\frac{\varepsilon {\varepsilon }_0S}{d}\left(6\right),\]где $S$ -- площадь обкладки, $d$ -- расстояние между пластинами, $\varepsilon $ -- диэлектрическая проницаемость вещества. Чем меньше $d$, тем больше совпадает расчётная емкость конденсатора (6), с реальной емкостью.
Емкость цилиндрического конденсатора равна:
\[C=\frac{2\pi \varepsilon {\varepsilon }_0l}{{ln \left({R_2}/{R_1}\right)\ }}\left(7\right),\]где $l$- высота цилиндра, $R_1$ и $R_2$ -- радиусы обкладок.
Емкость сферического конденсатора можно рассчитать по формуле:
\[C=4\pi \varepsilon {\varepsilon }_0\frac{R_1R_2}{R_2-R_1}\ \left(8\right),\]где $R_1{\ и\ R}_2$ -- радиусы обкладок конденсатора.
Любой конденсатор, еще характеризуется предельным напряжением $U_{max}$, это такое максимальное напряжение, которое может быть приложено к конденсатору и пробоя не будет.
Задание: Получите формулу для расчета емкости сферического конденсатора, диэлектрическая проницаемость вещества между обкладками равно $\varepsilon .$
Решение:
Емкость любого конденсатора можно вычислить как:
\[C=\frac{q}{{\varphi }_1-{\varphi }_2}\left(1.1\right).\]Сферический конденсатор состоит из 2 концентрических проводящие сфер, пространство между ними диэлектрик (рис.1). Обкладки эти сфер несут заряд +q и --q. Выделим сферическую поверхность радиуса r, такую, что $R_1\le r\le R_2$ (на рис.1 изображена пунктиром).
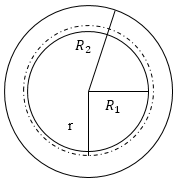
Рис. 1
Напряженность электростатического поля, которое создает внутренняя обкладка конденсатора на расстоянии r от нее (во всех точках выделенной сферы), может быть записана как:
\[E=\frac{q}{4\pi \varepsilon {\varepsilon }_0r^2}\left(1.2\right).\]Найдем ${\varphi }_1-{\varphi }_2$ между обкладками конденсаторов, через напряженность:
\[{\varphi }_1-{\varphi }_2=\int\limits^{R_2}_{R_1}{Edr}=\frac{q}{4\pi \varepsilon {\varepsilon }_0}\int\limits^{R_2}_{R_1}{\frac{dr}{r^2}}=-\frac{q}{4\pi \varepsilon {\varepsilon }_0}\left(\frac{1}{R_2}-\frac{1}{R_1}\right)=\frac{q{(R}_1-R_2)}{4\pi \varepsilon {\varepsilon }_0R_1R_2}(1.3)\]В таком случае подставляем в (1.1) выражение из (1.3), получаем:
\[C=\frac{q4\pi \varepsilon {\varepsilon }_0R_1R_2}{q{(R}_1-R_2)}=\frac{4\pi \varepsilon {\varepsilon }_0R_1R_2}{{(R}_1-R_2)}.\]Ответ: Для сферического конденсатора $C=\frac{4\pi \varepsilon {\varepsilon }_0R_1R_2}{{(R}_1-R_2)}.$
Задание: Площадь пластин плоского конденсатора равна $S$. Напряжение между его пластинами равно $U$, заряд пластин равен $q$. Найдите, на каком расстоянии расположены пластины?
Решение:
Напряженность поля плоского конденсатора равна:
\[E=\frac{\sigma}{\varepsilon {\varepsilon }_0}\ \left(2.1\right),\]где поверхностная плотность заряда равна $\sigma=\frac{q}{S}.$
С другой стороны напряженность можно выразить как:
\[E=\frac{U}{d}\left(2.2\right).\]Приравняем правые части уравнений (2.1) и (2.2), получим:
\[\frac{\sigma}{\varepsilon {\varepsilon }_0}=\frac{q}{S\varepsilon {\varepsilon }_0}=\frac{U}{d}\ \left(2.3\right).\]Из (2.3) выразим расстояние между пластинами, получим:
\[d=\frac{SU\varepsilon {\varepsilon }_0}{q}.\]Ответ: $d=\frac{SU\varepsilon {\varepsilon }_0}{q}.$











