Электрический заряд
В соответствии с современными представлениями атомы всех тел построены из электрически заряженных частиц. Относительно легких электронов и довольно тяжелых положительно заряженных атомных ядер. В целом тела электрически нейтральны, так как суммарный отрицательный заряд электронов равен суммарному положительному заряду атомных ядер данного тела. Отрицательный заряд электрона равен (так как к этой величине прибегают довольно часто, то заряд электрона часто имеет свое обозначение $q_e$ или $e$) $e=1,6\cdot {10}^{-16}Кл$ (в системе СИ) или $e=4,8\cdot {10}^{-10}$ абсолютных электростатических единиц электричества (в СГСЭ). Положительные заряды атомных ядер равны по модулю целым, кратным элементарному заряду (так еще называют заряд электрона), то есть заряд ядра: $q=ne$, где $n$- целое число. Масса электрона равна $m_e=9.1\cdot {10}^{-31}кг$. Самым лёгким ядром является ядро атома водорода, которое именуется протоном. Его масса равна $m_p=1.67\cdot {10}^{-27}кг$. Размеры атомных ядер, электронов малы по сравнению с расстояниями между ними в атомах и молекулах, что позволяет во многих случаях считать их материальными точками, которые имеют массу и электрический заряд.
Мысль о дискретности электрического заряда была высказана уже Б. Франклином в 1752 г. Экспериментом она подтверждена Фарадеем, при исследовании законов электролиза. Однако окончательный вывод о дискретности электрического заряда был сделан Г.Л. Гельмгольцем и Д. Стонеем в 1881 г. Количественное значение элементарного заряда было вычислено на основании законов электролиза. Прямое экспериментальное измерение элементарного заряда было сделано Р.Э. Милликеном в 1909 г. Были предприняты поиски дробных зарядов, но они дали отрицательный результат. Сделаем вывод, на сегодняшний момент установлено, что дробных зарядов в свободном состоянии не существует.
Независимость количественного значения элементарного заряда от скорости доказывается фактом нейтральности атомов. Электроны в атоме движутся значительно быстрее протонов (это следствие различая масс). В том случае, если бы заряд зависел от скорости, то нейтральность атомов нарушалась. Инвариантность заряда относительно скорости -- одно из экспериментальных обоснований теории электричества.
В большинстве макроскопических явлений участвует очень большое количество электрических зарядов, в таком случае их дискретность значения не имеет, и в большинстве случаев можно считать, что заряд как бы непрерывно распределён в пространстве.
Объемная плотность распределения
Объемной плотностью распределения зарядов называют отношение:
где $\triangle Q$- полный заряд, находящийся в объеме $\triangle V$, $e_i$ -- элементарный заряд, $\triangle V$ -- малый объем, но не бесконечно малый в математическом смысле, он характеризуется координатой точки внутри него. Это значит, что можно записать: $\rho =\rho \left(x,y,z\right).$ При определении объемной плотности $\rho $ можно рассматривать как функцию, а заряд считать непрерывно распределенным, тогда можно записать, что:
где $dV$- дифференциал объема.
Концентрацией зарядов (n) называют отношение:
где ∆n -- количество зарядов в объеме $\triangle V$.
Поверхностной плотностью заряда ($\sigma$) называется соотношение:
где $\triangle S$- малая площадь поверхности, $\triangle Q$ -- заряд, находящийся на поверхности $\triangle S$. Полный заряд поверхности, при условии равномерного распределения заряда по ней, можно найти как:
где $dS$ -- дифференциал площади поверхности.
Закон сохранения заряда
Закон сохранения заряда приведем в двух формах. Одна из них следующая. Она исходит из двух фактов:
- Электрон и протон -- материальные частицы с бесконечным временем жизни, их заряды инвариантны и не зависят от скорости. В такой трактовке, закон сохранение -- следствие неуничтожимой носителей заряда.
- Кроме протонов и электронов существуют другие заряженные элементарные частицы. Все они рождаются, порождают другие частицы, участвуют в процессах взаимных превращений, но какими бы ни были превращения, суммарный заряд частиц до равен суммарному заряду после взаимопревращений.
Таким образом, закон сохранения заряда может быть сформулирован следующим образом:
Заряд сохраняется при всех процессах и движениях носителей зарядов.
Здесь надо отметить, что имея некоторую самостоятельность, заряд не может существовать отдельно от его носителя - материи.
Закон сохранения заряда можно записать в интегральной форме. Изменение заряда в некотором объеме V может произойти только в результате втекания или вытекания заряда через замкнутую поверхность $S$, которая ограничивает объем $V$. Или в математическом виде:
где сила тока, протекающая через замкнутую поверхность S равна интегралу по этой поверхности:
где $\overrightarrow{j}\cdot d\overrightarrow{S}=jdScos(\widehat{\overrightarrow{j}\cdot d\overrightarrow{S}})$, j -- плотность тока $\overrightarrow{j}=\frac{1}{\triangle V}\sum\limits_{\triangle V}{e_i{\overrightarrow{v}}_i}$, ${\overrightarrow{v}}_i$ -- скорость элементарного заряда, $d\overrightarrow{S}$ направлен по внешней нормали к поверхности.
$\frac{\partial }{\partial t}\int\nolimits_V{\rho dV}$- скорость изменения заряда в объеме. Знак минус в формуле (6) указывает на то, что если положительный заряд внутри объема уменьшатся, то плотность тока направлена из объема $V$.
Дифференциальная форма закона сохранения заряда (оно же уравнение непрерывности) имеет вид:
Напомним, что $div\overrightarrow{j}=\frac{\partial j_x}{\partial x}+\frac{\partial j_y}{\partial y}+\frac{\partial j_z}{\partial z}$.
Схема опытов Милликена изображена на рис. 1. Маленькие заряженные шарообразные частицы (капельки масла) движутся в воздухе при наличии однородного электрического поля $\overrightarrow{E}.$ На частицу действуют следующие силы: силы тяжести ($\ \ {\rho }_{ch}>{\rho }_{vozd},\ плотность\ частицы\ \left(\ {\rho }_{ch}\right),\ плотность\ воздуха\ ({\rho }_{vozd})$), сила вязкого трения, электростатическая сила, сила Архимеда. Сила вязкого трения пропорциональна скорости, следовательно, при постоянной скорости частицы сумма действующих на частицу сил равна нулю. Все силы, помимо электрической измерялись экспериментально при движении частицы в отсутствии электрического поля. Исследовав движение частицы в поле, Милликен нашел силу $q\overrightarrow{E}.$ Это позволило вычислить заряд частицы, так как напряженность поля известна. Изменяя напряженность поля можно добиться, чтобы заряженная частица находилась в покое.
Задание: В электростатическое поле впрыскивают заряженную каплю масла (плотность масла считать известной, равной ${\rho }_{ch}$) радиуса R. Напряжённость поля (E) подбирают такой, чтобы капля масла оставалась неподвижной. Капля находится в воздухе, плотность воздуха ${\rho }_{vozd}$. Определите заряд капли.
Решение:
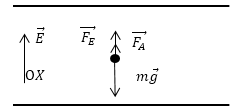
Рис. 1
Если скорость частицы равна нулю, то сила вязкого трения также равна нулю.
Запишем второй закон Ньютона для заряженной капельки масла, если мы знаем, что частица неподвижна:
\[m\overrightarrow{g}+\overrightarrow{F_A}+\overrightarrow{F_E}=0\left(1.1\right).\]Направим ось ОX вдоль поля, запишем проекцию уравнения (1.1) на эту ось:
\[F_A+F_E-mg=0\ \left(1.2\right),\]где $F_A$ сила Архимеда, которая равна:
\[F_A=с_{vozd}Vg=с_{vozd}\frac{4}{3}\pi R^3g\ \left(1.3\right),\]$R$ -- радиус капли масла.
$F_E$ -- электростатическая сила, действующая на заряженную каплю со стороны поля:
\[F_E=qE\ \left(1.4\right),\]где $q$ -- заряд капли масла, $E$ -- напряженность электростатического поля.
$mg$- сила тяжести, действующая на каплю, ее можно выразить через плотность масла:
\[mg=с_{ch}\frac{4}{3} \pi R^3g\ \left(1.5\right).\]Подставим выражения (1.3) -- (1.5) в уравнение (1.2), получим:
\[{\rho }_{vozd}\frac{4}{3}\pi R^3g\ +qE-{\rho }_{ch}g\frac{4}{3}\pi R^3=0\ \left(1.6\right).\]Выразим из (1.6) заряд капли:
\[q=\frac{{\rho }_{ch}g\frac{4}{3}\pi R^3-{\rho }_{vozd}\frac{4}{3}\pi R^3g}{E}=\frac{\frac{4}{3}{\pi R^3(\rho }_{ch}-{\rho }_{vozd})g}{E}\]Ответ: Заряд капли масла должен быть $q=\frac{\frac{4}{3}{\pi R^3(\rho }_{ch}-{\rho }_{vozd})g}{E}$.
Задание: Два одинаковых металлических шарика имею заряды $q_1$ и $q_2$ одинаковые по знаку. Их соединили, а за тем развели. Чему будут равны заряды каждого из шариков после разъединения.
Решение:
Основа для решения -- закон сохранения заряда, запишем его для нашего случая:
\[q_1+q_2={q'}_1+{q'}_2\ \left(2.1\right).\]Так как шарики одинаковые можем записать, что суммарный заряд шариков $q_1+q_2$ разделится поровну между ними, то есть:
\[{q'}_1=\frac{q_1+q_2}{2},\ {q'}_2=\frac{q_1+q_2}{2}.\]Ответ: Заряд каждого шарика станет равен q=$\frac{q_1+q_2}{2}$.












