
Теорема о циркуляции
Ранее мы выяснили, что на заряд (q), который находится в электростатическом поле, действуют консервативные силы, работа ($A$) которых на любом замкнутом пути (L) равна нулю:
где $\overrightarrow{s}$- вектор перемещения (не путать с площадью), $\overrightarrow{E}$ -- вектор напряженности поля.
Для единичного положительного заряда можем записать:
Интеграл в левой части уравнения (2) есть циркуляция вектора напряженности по контуру L. Характерным свойством электростатического поля является то, что циркуляция его вектора напряжённости по любому замкнутому контуру равна нулю. Такое утверждение называется теоремой о циркуляции вектора напряженности электростатического поля.
Докажем теорему о циркуляции на том основании, что работа поля по перемещению заряда не зависит от траектории перемещения заряда в электростатическом поле, что выражается равенством:
где $L_1\ и\ L_2$ различные пути между точками А и В. Учтем, что при замене местами пределов интегрирования получим:
Выражение (4) представим как:
где $L=L_1+L_2$. Так теорема доказана.
Следствие теоремы о циркуляции
Следствием теоремы о циркуляции является то, что линии напряженности электростатического поля незамкнуты. Они начинаются на положительных зарядах, а заканчиваются на отрицательных или уходят в бесконечность. Теорема верна именно для статичных зарядов. Другое следствие теоремы: непрерывность тангенциальных составляющих напряженности (в отличие от нормальных составляющих). Это значит, что компоненты напряженности, которые являются касательными к выбранной любой поверхности во всякой ее точке, имеют по обе стороны поверхности равные значения.
Выделим произвольную поверхность S, которая опирается на контур L (рис.1).
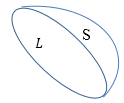
Рис. 1
В соответствии с формулой Стокса (теоремой Стокса) интеграл от ротора вектора напряженности ($rot\overrightarrow{E}$), взятый по поверхности S равен циркуляции вектора напряженности вдоль контура, на который опирается данная поверхность:
где $d\overrightarrow{S}=dS\cdot \overrightarrow{n}$, $\overrightarrow{n}$ -- единичный вектор перпендикулярный участку dS. Ротор ($rot\overrightarrow{E}$) характеризует интенсивность «завихрения» вектора. Наглядное представление о роторе вектора можно получить, если маленькую легкую крыльчатку (рис.2) поместить в поток жидкости. В тех местах, где ротор не равен нулю, крыльчатка будет вращаться, причем скорость ее вращения будет тем больше, чем больше проекция модуль проекции ротора на ось крыльчатки.
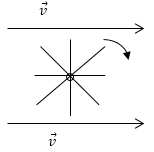
Рис. 2
При практическом вычислении ротора чаще других используют формулы:
Так как в соответствии с уравнением (6) циркуляция вектора напряжённости равна нулю, то мы получаем:
Условие (8) должно выполняться для любой поверхности S, которая опирается на контур L. Это возможно только в том случае, если подынтегральное выражение:
причем для каждой точки поля.
По аналогии с крыльчаткой на рис. 2 представим себе электрическую «крыльчатку». На концах такой «крыльчатки» расположены одинаковые по величине заряды q. Система помещена в однородное поле с напряженностью E. В тех местах, где $rot\overrightarrow{E}\ne 0$ такое «устройство» будет вращаться с ускорением, которое зависит от проекции ротора на ось крыльчатки. В случае, электростатического поля такое «устройство» не стало бы вращаться ни при какой ориентации оси. Так как отличительной особенностью электростатического поля является то, что оно безвихревое. Уравнение (9) представляет теорему о циркуляции в дифференциальной форме.
Задание: На рис. 3 изображено электростатическое поле. Что можно сказать о характеристиках данного поля из рисунка?
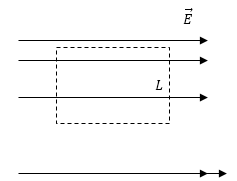
Рис. 3
Решение:
О данном поле можно сказать, что существование такого электростатического поля невозможно. Если выделить контур (он изображен пунктиром). Для такого контура циркуляция вектора напряженности:
\[\oint\limits_L{\overrightarrow{E}d\overrightarrow{s}\ne 0}\left(1.1\right),\]что противоречит теореме о циркуляции для электростатического поля. Напряженность поля определяется густотой силовых линий, она в разных частях поля не одинакова, в результате работа по замкнутому контуру будет отличаться от нуля, следовательно, циркуляция вектора напряженности не равна нулю.
Задание: Исходя из теоремы о циркуляции, покажите, что тангенциальные составляющие вектора напряженности электростатического поля не изменяются при переходе через границу раздела диэлектриков.
Решение:
Рассмотрим границу между двумя диэлектриками с диэлектрическими проницаемостями ${\varepsilon }_2\ и\ {\varepsilon }_1$ (рис.4). Выберем на этой границе небольшой прямоугольный контур с параметрами a - длина, b - ширина. Ось Х проходит через середины сторон b.
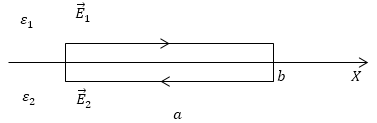
Рис. 4
Для электростатического поля выполняется теорема о циркуляции, которая выражается уравнением:
\[\oint\limits_L{\overrightarrow{E}d\overrightarrow{s}=0\ \left(2.1\right).}\]При небольших размерах контура циркуляция вектора напряженности и в соответствии с указанным направлением обхода контура интеграл в формуле (2.1) можно представить как:
\[\oint\limits_L{\overrightarrow{E}d\overrightarrow{s}=E_{1x}a-E_{2x}a+\left\langle E_b\right\rangle 2b=0\ \left(2.2\right),}\]где $\left\langle E_b\right\rangle $- среднее значение $\overrightarrow{E}$ на участках перпендикулярных к границе раздела.
Из (2.2) следует, что:
\[{(E}_{2x}-E_{1x})a=\left\langle E_b\right\rangle 2b\ (2.3).\]Если $b\to 0$, то получаем, что:
\[E_{2x}=E_{1x}\ \left(2.4\right).\]Выражение (2.4) выполняется при произвольном выборе оси X, которая лежит на границе раздела диэлектриков. Если представить вектор напряженности в виде двух составляющих (тангенциальной $E_{\tau }\ $ и нормальной $E_n$):
\[\overrightarrow{E_1}=\overrightarrow{E_{1n}}+\overrightarrow{E_{1\tau }},\overrightarrow{E_2}=\overrightarrow{E_{2n}}+\overrightarrow{E_{2\tau }}\ \left(2.5\right).\]В таком случае из (2.4) запишем:
\[E_{\tau 1}=E_{\tau 2}\ \left(2.6\right),\]где $E_{\tau i}$- проекция вектора напряженности на орт $\tau $, направленный вдоль границы раздела диэлектриков.











