Что такое электростатика
Электростатикой называют раздел физики, который изучает свойства и взаимодействия электрических зарядов которые неподвижны относительно избранной инерциальной системы отсчета.
Согласно теории близкодействия взаимодействие между частицами или макротелами осуществляется посредством физических полей, создаваемых этими телам (частицами). Соответственно, электростатика изучает и электростатические поля и их свойства. Электростатическое поле представляет собой неизменное во времени электрическое поле, которое создается неподвижными зарядами. Электростатическое поле -- частный случай электромагнитного поля. Электростатические поля имеют характеристики, например, напряженность ($\overrightarrow{E}$), потенциал ($\varphi $), энергия. Поля могут быть изображены графически, при этом используются силовые линии поля. Силовыми линиями поля, называют линии, касательными к которым в каждой точке поля являются векторы напряженности. Силовые линии электростатического поля разомкнуты (они начинаются на положительных зарядах, а оканчиваются на отрицательных). Силовые линии электростатического поля нигде не пересекаются. Основной задачей электростатики является отыскание векторов напряженности в каждой точке поля, которое создано системой зарядов -- источников электростатического поля. Для решения этой задачи применяют принцип суперпозиции:
\[\overrightarrow{E}=\sum\nolimits_n{{\overrightarrow{E}}_i\ (1)}\]и метод, основанный на вычислении потоков вектора напряженности электростатического поля:
\[Ф_E=\oint\limits_S{\overrightarrow{E}d\overrightarrow{S}=\frac{Q}{{\varepsilon }_0}}\ \left(2\right),\]где $Ф_E$- поток вектора напряженности через замкнутую поверхность $S$, $Q$ - суммарный заряд, находящийся внутри этой поверхности.
Основы электростатики
Основы электростатики заложил Кулон, правда, надо отметить, что еще до Кулона подобные выводы относительно электростатического поля были сделаны Кавендишем, но он работы не публиковал, его выводы хранились в семейной библиотеке и были представлены на обозрение миру лишь его семьей. Кулон предположил, что заряженные тела взаимодействуют на расстоянии. В своих опытах Кулон измерял силы взаимодействия заряженных шаров и сделал вывод, что модуль силы взаимодействия двух неподвижных точечных заряженных объектов пропорционален произведению модулей их зарядов, обратно пропорционален квадрату расстояния между телами. Математическая запись закона Кулона для тел в вакууме имеет вид:
\[F_e=k\frac{q_1q_2}{r^2}\ \left(3\right),\]сила $\overrightarrow{F_e}$ направлена вдоль прямой, которая соединяет заряженные тела. В системе СИ $k=9\cdot 10^9\frac{Нм^2}{Кл^2}$.
Базовым законом в электростатике является закон сохранения заряда, согласно которому в замкнутой системе алгебраическая сумма зарядов остаётся постоянной:
\[\sum\limits_n{q_i=const\ \left(4\right).}\]Фарадей внёс существенный вклад в развитие электростатики. Он установил роль диэлектриков в электростатических явлениях. Фарадей ввел в электростатику представление о силовых линиях поля, высказал мысль о конечной скорости распространения электрической энергии.
Теория Максвелла
Максвелл повторил опыты Кавендиша и Фарадея, перевел идей Фарадея в математическую форму. Система уравнений Максвелла является обобщением основных законов об электрических и электромагнитных явлениях. Она описывает абсолютно все электромагнитные явления. Являясь основой теории электромагнитного поля, эта система уравнений позволяет решать задачи, связанные с отысканием электрических и магнитных полей, создаваемых заданным распределением электрических зарядов и токов. Уравнения Максвелла были отправной точкой для создания общей теории относительности Эйнштейна. В теории Максвелла раскрывается электромагнитная природа света. Уравнения сформулированы Дж. Максвеллом в шестидесятых годах 19 века на основе обобщения эмпирических законов и развития идей ученых, исследовавших электромагнитные явления до него (Законы Кулона, Био -- Савара, Ампера и, в особенности, исследования Фарадея). Сам Максвелл записал 20 уравнений с 20 неизвестными в дифференциальной форме, которые позднее были преобразованы. Современная форма Максвелла дана немецким физиком Г. Герцем и английским физиком О. Хевисайдом.
Задание: В формуле Кулона, которая записана в системе СИ, коэффициент пропорциональности $k=9\cdot 10^9\frac{Н{\cdot м}^2}{Кл^2}$. Каким станет этот коэффициент, если основные единицы: длины, силы, тока и массы увеличить в n раз?
Решение:
Чтобы решить эту задачу внимательно исследуем размерность коэффициента $k.$ Она имеет вид:
\[\frac{Н{\cdot м}^2}{Кл^2}\left(1.1\right).\]Известно, что кулон -- это заряд, который проходит через поперечное сечение проводника в единицу времени при силе тока 1 А, так как:
\[\triangle q=I\triangle t\ \left(1.1\right).\]Следовательно,
\[\left[\triangle q\right]=А\cdot с.\]Если по условию задачи мы увеличиваем обозначенные в условии единицы:
\[\frac{n(Н){\cdot n^2(м}^2)}{n^2(A^2c^2)}\to n\]Ответ: Коэффициент пропорциональности в законе Кулона станет $n\cdot k$.
Задание: Заряженные шарики массы $m_1=m_2=m\ $подвешены на нитях одинаковой длины в одной точке, их заряды равны $q_1$ и $q_2$.(рис.1). Какова должна быть диэлектрическая проницаемость жидкости, чтобы при погружении в нее системы из шариков угол расхождения нитей не изменился? Отношение плотности шариков к плотности диэлектрика ($\frac{{\rho }_{sh}}{{\rho }_d}$)=a.
Решение:
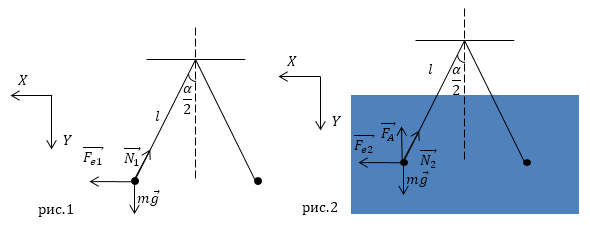
Запишем условие равновесия шарика (одного) в воздухе:
\[\overrightarrow{F_{e1}}+\overrightarrow{mg}+\overrightarrow{N_1}=0\ \left(2.1\right).\]Запишем условие равновесия шарика (одного) в жидкости:
\[\overrightarrow{F_{e2}}+\overrightarrow{mg}+\overrightarrow{N_2}+\overrightarrow{F_A}=0\ \left(2.2\right).\]Запишем проекции уравнения (2.1.) на оси:
Ох: $F_{e1}-N_1sin(\frac{\alpha }{2})$=0 (2.3),
Oy: $mg-N_1cos(\frac{\alpha }{2})$=0 (2.4).
Проекции уравнения (2.2) на оси:
Ох: $F_{e2}-N_2sin(\frac{\alpha }{2})$=0 (2.5),
Oy: $mg-N_2cos{s \left(\frac{\alpha }{2}\right)\ }-F_A=0\ \left(2.6\right)$.
Разделим уравнение (2.3) на (2.4), получим:
\[tg\left(\frac{\alpha }{2}\right)=\frac{F_{e1}}{mg}\ \left(2.7\right).\]Уравнение (2.5) на уравнение (2.6), имеем:
\[tg\left(\frac{\alpha }{2}\right)=\frac{F_{e2}}{mg-F_A}\to \frac{F_{e1}}{mg}=\frac{F_{e2}}{mg-F_A}\left(2.8\right).\]По закону Кулона запишем выражения для $F_{e1},\ F_{e2}$:
\[F_{e1}=\frac{q_1q_2}{4\pi {\varepsilon }_1{\varepsilon }_0r^{2\ \ }}и\ F_{e2}=\frac{q_1q_2}{4\pi {\varepsilon }_2{\varepsilon }_0r^{2\ \ }}\ \left(2.9\right).\]Модуль силы Архимеда равен:
\[F_A={\rho }_dVg={\rho }_d\frac{m}{{\rho }_{sh}}g\ \left(2.10\right).\]Подставим в уравнение (2.8) уравнения (2.9) и (2.10), получим:
\[\frac{\frac{q_1q_2}{4\pi {\varepsilon }_1{\varepsilon }_0r^{2\ \ }}}{mg}=\frac{\frac{q_1q_2}{4\pi {\varepsilon }_2{\varepsilon }_0r^{2\ \ }}}{mg-{\rho }_d\frac{m}{{\rho }_{sh}}g\ }\to \frac{\frac{1}{{\varepsilon }_1}}{1}=\frac{\frac{1}{{\varepsilon }_2}}{1-\frac{{\rho }_d}{{\rho }_{sh}}\ }\to {\varepsilon }_2=\frac{{\varepsilon }_1}{1-\frac{{\rho }_d}{{\rho }_{sh}}}=\frac{{\varepsilon }_1}{1-a}.\]Считаем, что ${\varepsilon }_1=1$ так как первоначально шарики находились в воздухе. Можно считать задачу решенной.
Ответ: Диэлектрическая проницаемость жидкости должна быть ${\varepsilon }_2=\frac{е_1}{1-a}$.












