Колебаниями называют любые периодические движения. Если при таких движениях изменения какой- либо величины описывают с помощью законов синуса или косинуса, то такие колебания называют гармоническими. Рассмотрим контур, из конденсатора (который перед включением в цепь зарядили) и катушки индуктивности (рис.1).
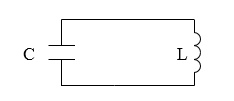
Рисунок 1.
Уравнение гармонических колебаний можно записать следующим образом:
$q=q_0cos({\omega }_0t+{\alpha }_0)$ (1)
где $t$-время; $q$ заряд, $q_0$-- максимальное отклонение заряда от своего среднего (нулевого) значения в ходе изменений; ${\omega }_0t+{\alpha }_0$- фаза колебаний; ${\alpha }_0$- начальная фаза; ${\omega }_0$- циклическая частота. За период фаза меняется на $2\pi $.
Уравнение вида:
уравнение гармонических колебаний в дифференциальном виде для колебательного контура, который не будет содержать активного сопротивления.
Любой вид периодических колебаний можно точности представить как сумму гармонических колебаний, так называемого гармонического ряда.
Для периода колебаний цепи, которая состоит из катушки и конденсатора мы получим формулу Томсона:
Если мы продифференцируем выражение (1) по времени, то можем получить формулу фунци $I(t)$:
Напряжение на конденсаторе, можно найти как:
Из формул (5) и (6) следует, что сила тока опережает напряжение на конденсаторе на $\frac{\pi }{2}.$
Гармонические колебания можно представлять как в виде уравнений, функций так и векторными диаграммами.
Уравнение (1) представляет свободные незатухающие колебания.
Уравнение затухающих колебаний
Изменение заряда ($q$) на обкладках конденсатора в контуре, при учете сопротивления (рис.2) будет описываться дифференциальным уравнением вида:
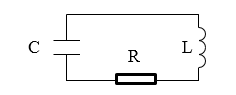
Рисунок 2.
Если сопротивление, которое входит в состав контура $R \[q=A_0e^{\left(-\beta t\right)}{sin \left(\omega t+{\alpha }_0\right)\left(7\right),\ }\]
где $\omega =\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}$ -- циклическая частота колебаний. $\beta =\frac{R}{2L}-$коэффициент затухания. Амплитуда затухающих колебаний выражается как:
В том случае, если при $t=0$ заряд на конденсаторе равен $q=q_0$, тока в цепи нет, то для $A_0$ можно записать:
Фаза колебаний в начальный момент времени (${\alpha }_0$) равна:
При $R >2\sqrt{\frac{L}{C}}$ изменение заряда не является колебаниями, разряд конденсатора называют апериодическим.
Задание: Максимальное значение заряда равно $q_0=10\ Кл$. Он изменяется гармонически с периодом $T= 5 c$. Определите максимально возможную силу тока.
Решение:
В качестве основания для решения задачи используем:
\[q=q_0cos\left({\omega }_0t+{\alpha }_0\right)\left(1.1\right).\]Для нахождения силы тока выражение (1.1) необходимо продифференцировать по времени:
\[I=-q_0{\omega }_0{sin \left({\omega }_0t+{\alpha }_0\right)\left(1.2\right),\ }\]где максимальным (амплитудным значением) силы тока является выражение:
\[I_0=q_0{\omega }_0\ \left(1.3\right).\]Из условий задачи нам известно амплитудное значение заряда ($q_0=10\ Кл$). Следует найти собственную частоту колебаний. Ее выразим как:
\[{\omega }_0=\frac{2\pi }{T}\left(1.4\right).\]В таком случае искомая величина будет найдена при помощи уравнений (1.3) и (1.2) как:
\[I_0=q_0\frac{2\pi }{T}.\]Так как все величины в условиях задачи представлены в системе СИ, проведем вычисления:
\[I_0=10\frac{2\cdot 3,14}{5}=12,56\ (А).\]Ответ: $I_0=12,56\ А.$
Задание: Каков период колебаний в контуре, который содержит катушку индуктивности $L=1$Гн и конденсатор, если сила тока в контуре изменяется по закону: $I\left(t\right)=-0,1sin20\pi t\ \left(A\right)?$ Какова емкость конденсатора?
Решение:
Из уравнения колебаний силы тока, которое приведено в условиях задачи:
\[I\left(t\right)=-0,1sin20\pi t\left(2.1\right)\]мы видим, что ${\omega }_0=20\pi $, следовательно, мы можем вычислить период Колебаний по формуле:
\[T=\frac{2\pi }{{\omega }_0}\left(2.2\right).\] \[T=\frac{2\pi }{20\pi }=0,1\left(c\right).\]По формуле Томсона для контура, который содержит катушку индуктивности и конденсатор, мы имеем:
\[T=2\pi \sqrt{LC}\to C=\frac{T^2}{4{\pi }^2L}\left(2.3\right).\]Вычислим емкость:
\[C=\frac{{0,1}^2}{4{\cdot 3,14}^2\cdot 1}=2,5\cdot {10}^{-4}\left(Ф\right).\]Ответ: $T=0,1$ c, $C=2,5\cdot {10}^{-4}Ф.$











