Рассмотрим $R-L-C$ контур (рис.1), где $R$-сопротивление, $L$ -- индуктивность -- $C$ -- емкость. Допустим, что сила тока ($I$) во всех сечениях контура одинакова (вне конденсатора -- это ток проводимости, между обкладками конденсатора -- это ток смещения).
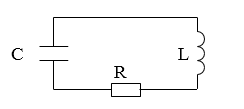
Рисунок 1.
Заряды обкладок конденсатора равны $q$, емкость конденсатора много больше, чем емкость всех остальных составных частей контура, индуктивностью проводов и всего остального можно пренебречь в сравнении с индуктивностью катушки. Кроме того, будем считать, что общая энергия электрического поля практически равна энергии участка, который заключен между обкладками конденсатора. В том случае, если поле квазистационарно, то мгновенное значение этой энергии зависит от мгновенного значения заряда на конденсаторе, аналогично со статическим случаем. Подобным образом можно сформулировать зависимость величины магнитной энергии от силы тока в цепи. Общая электромагнитная энергия системы (рис.1) будет выражена формулой:
Энергия колебательного контура при свободных и незатухающих колебаниях
Если электромагнитные колебания являются свободными и незатухающими, то в контуре происходит периодический переход электрической энергии конденсатора в магнитную энергию электрического тока и наоборот. В моменты времени, равные $t=0,\ \frac{T}{2},\ T\ \dots $ энергия электрического поля является максимальной ($W_q$), а энергия магнитного поля ($W_m$) равна нулю:
В моменты времени равные $t=\ \frac{T}{4},\ \frac{3T}{4}\ \dots энергия\ магнитного\ поля\ \left(W_m\right)$ максимальна, энергия электрического поля $W_qравна\ нулю:$
получаем, что:
где величина $\sqrt{L/C}$ -- волновое сопротивление контура.
Если колебательный контур имеет сопротивление, то для того, чтобы колебания не были затухающими к контуру подводят энергию, которая компенсирует затраты на джоулево тепло. Такие колебания называют вынужденными.
Задание: Используя формулу для энергии, запасенной в колебательном контуре, получите уравнение колебаний силы тока.
Решение:
Формулу для энергии, запасенной в колебательном контуре ($W=\frac{q^2}{2C}+\frac{{LI}^2}{2}.$) удобно использовать для того, чтобы получить дифференциальное уравнение колебаний силы тока в данной системе. Отметим, что количество джоулева тепла ($Q=I^2R$), которое выделяется в контуре равно убыли электромагнитной энергии, то есть:
\[I^2R=-\frac{dW}{dt}\left(1.1\right).\]Воспользуемся уравнением (1), подставим энергию, запасенную в контуре в формулу (1.1), получим:
\[I^2R=-\frac{d}{dt}\left(\frac{q^2}{2C}+\frac{{LI}^2}{2}\right)=-(\frac{q}{C}\frac{dq}{dt}+LI\frac{dI}{dt})\left(1.2\right).\]Заметим, что сила тока равна убыли заряда на обкладках конденсатора:
\[I=-\frac{dq}{dt}\left(1.3\right).\]В соответствии с уравнением (1.3) преобразуем формулу (1.2), следовательно, имеем:
\[I^2R=\frac{q}{C}I-LI\frac{dI}{dt}\to IR=\frac{q}{C}-L\frac{dI}{dt}\left(1.4\right).\]Продифференцируем уравнение (1.4) по времени, используем соотношение (1.3), получим:
\[L\frac{d^2I}{dt^2}+R\frac{dI}{dt}+\frac{1}{C}I=0\left(1.5\right).\]Формула (1.5) известна как уравнение затухающих периодических колебаний. Общее решения уравнения (1.5) имеет вид:
\[I=Ae^{k_1t}+Be^{k_2t}\left(1.6\right),\]где $A$ и $B$ -- произвольные постоянные интегрирования, $k_1{,k}_2$ -- корни квадратного уравнения:
\[Lk^2+Rk+\frac{1}{C}=0\ \left(1.7\right),\]то есть:
\[k=-\frac{R}{2LC}\pm \sqrt{{\left(\frac{R}{2LC}\right)}^2-\frac{1}{LC}}\left(1.8\right).\]В том случае, если ${\left(\frac{R}{2LC}\right)}^2-\frac{1}{LC} >0$, то $k$ -- имеют вещественные, отрицательные значения. При таком условии разряд конденсатора будет апериодическим. В том случае, если ${\left(\frac{R}{2LC}\right)}^2-\frac{1}{LC} \[\omega =\sqrt{\frac{1}{LC}-{\left(\frac{R}{2L}\right)}^2}\left(1.9\right).\]
Используя введённое обозначение (1.9), получим:
\[k=\frac{R}{2L}\pm i\omega \ \left(1.10\right).\]Уравнение колебаний запишем как:
\[I=Ae^{k_1t}+Be^{k_2t}=e^{-\frac{R}{2L}}\left(Ae^{i\omega t}+Be^{-i\omega t}\right)=ae^{-\frac{R}{2L}}{sin \left(\omega t+{\alpha }_0\right)\ },\]где $a$, ${\alpha }_0$ -- постоянные, которые зависят от постоянных интегрирования $A$ и $B$.
Ответ: $I\left(t\right)=ae^{-\frac{R}{2L}}{sin \left(\omega t+{\alpha }_0\right)\ }.$
Задание: В колебательном $RLC$- контуре, возбуждаются затухающие колебания собственной частоты $\omega$. Определите, через какое время энергия, запасенная в контуре, уменьшается в a раз? Считайте, что затухание идет очень медленно, а коэффициент затухания равен $\beta $.
Решение:
В качестве основы для решения используем выражение для энергии, запасённой в контуре:
\[W\left(t\right)=W_q+W_m\left(2.1\right),\]где $W_m=\frac{{LI}^2}{2}$- магнитная составляющая энергии контура, $W_q=\frac{q^2}{2C}=\frac{С{U_c}^2}{2}$ -- энергия электрическая. $U_c$- напряжение на конденсаторе, I -- сила тока в цепи. Условием малости затухания для данного контура является то, что:
\[\omega \gg \beta \ \left(2.2\right),\]где $\omega $ частота колебаний, $\beta $ -- коэффициент затухания колебаний. Если затухание мало, то напряжение и сила тока в $RLC$ контуре изменяется в соответствии с законами:
\[U_c\left(t\right)=U_0e^{-\beta t}{cos \left(\omega t\right)\ },\ I\left(t\right)=C\frac{dU_c}{dt}=\omega CU_0e^{-\beta t}{sin \left(\omega t\right)\ }\left(2.3\right).\]Тогда для энергии в соответствии с (2.1) получим:
\[W\left(t\right)=\frac{L}{2}\omega ^2C^2{U_0}^2e^{-2 \beta t}{{sin}^2 \left(\omega t\right)\ }+\frac{C}{2}{U_0}^2e^{-2 \beta t}{cos^2 \left(\omega t\right)=\ }\frac{C}{2}{U_0}^2e^{-2 \beta t}\left(2.4\right),\]где ${\omega }^2\approx \frac{1}{LC}.$ Начальное значение энергии в заданном контуре равно:
\[W\left(t=0\right)=\frac{C}{2}{U_0}^2\left(2.5\right).\]По условию задачи $\frac{W\left(t=0\right)}{W(t)}=a$, то:
\[\frac{W\left(t=0\right)}{W\left(t\right)}=\frac{\frac{C}{2}{U_0}^2}{\frac{C}{2}{U_0}^2e^{-2\beta t}}=\frac{1}{e^{-2\beta t}}=a\to e^{2\beta t}=a\to 2\beta t=lna\left(2.6\right).\]Из уравнения (2.6) получим, что энергия уменьшится через:
\[t=\frac{lna}{2\beta }.\]Ответ: $t=\frac{lna}{2\beta }.$











