Роль электромагнитных колебаний
Как известно, существуют несколько различных видов механического движения, колебания среди них занимают важное место. Колебаниями называют периодические (по времени) движения или процессы. Механические колебания лежат в основе измерения времени.
Аналогично этому, среди разного рода электрических явлений и процессов электромагнитные колебания занимают особое место. При таких колебаниях электровеличины (токи, заряды, поля и т.д.) изменяются периодически. Электромагнитные колебания широко используются в технике для реализации связи (телефонной, телеграфной и радиосвязи). Переменные токи, которые используют в технике, так же являются видом электрических колебаний. Световые явления -- электромагнитные колебания.
Колебательный контур и его основные характеристики
В механике простейшей колебательной системой является груз, который подвешен на пружине. Этот груз движется без трения. Массой подвеса пренебрегаю в сравнении с массой груза. Упругость считают сосредоточенной в пружине. Такая система совершает гармонические колебания, если ее вывели из состояния равновесия. При колебаниях кинетическая энергия переходит в потенциальную и обратно.
Аналогичные процессы можно наблюдать при электрических колебаниях. Простейшей колебательный контур, который рассматривают в электричестве состоит из конденсатора и катушки индуктивности, соединенных между собой. Считается, что емкость витков катушки мала в сравнении с емкостью конденсатора, а индуктивностью конденсатора и соединительных проводов можно пренебречь в сравнении с индуктивностью катушки. Такой контур называют закрытым или контуром с сосредоточенными емкостью и индуктивностью. Если считают, что в таком контуре сопротивление равно нулю, то его называют идеализированным. Колебания в этом контуре не затухают.
В общем случае в контур включают сопротивление ($R$), конденсатор емкостью $C$, катушку индуктивности $L$, тогда такой контур имеет вид указанный на рис.1. Колебания в таком контуре являются затухающими.
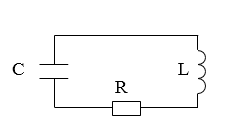
Рисунок 1.
Изменение заряда ($q$) на обкладках конденсатора в таком контуре описывается дифференциальным уравнением вида:
Если сопротивление, которое входит в состав контура $R \[q=A_0e^{\left(-\beta t\right)}{sin \left(\omega t+{\alpha }_0\right)\left(2\right),\ }\]
где $\omega =\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}$ -- циклическая частота колебаний. $\beta =\frac{R}{2L}-$коэффициент затухания. Амплитуда затухающих колебаний выражается как:
В том случае, если при $t=0$ заряд на конденсаторе равен $q=q_0$, тока в цепи нет, то для $A_0$ можно записать:
Начальная фаза колебаний (${\alpha }_0$) равна:
При $R>2\sqrt{\frac{L}{C}}$ изменение заряда не является колебаниями, разряд конденсатора называют апериодическим.
Свободные колебания. Вынужденные колебания
Свободные колебания заряда, силы тока и разности потенциалов называют свободными электромагнитными колебаниями.
Если электромагнитные колебания являются свободными и незатухающими, то в контуре происходит периодический переход электрической энергии конденсатора в магнитную энергию электрического тока и наоборот. В моменты времени, равные $t=0,\ \frac{T}{2},\ T\ \dots $ энергия электрического поля является максимальной ($W_q$), а энергия магнитного поля ($W_m$) равна нулю:
В моменты времени равные $t=\ \frac{T}{4},\ \frac{3T}{4}\ \dots энергия\ магнитного\ поля\ \left(W_m\right)$ максимальна, энергия электрического поля $W_q=0:$
получаем, что:
где величина $\sqrt{L/C}$ -- волновое сопротивление контура.
Если колебательный контур имеет сопротивление, то для того, чтобы колебания не были затухающими к контуру подводят энергию, которая компенсирует затраты на джоулево тепло. Такие колебания называют вынужденными.
Задание: Исходя из уравнений, которые описывают изменения заряда в колебательном контуре, напишите законы колебаний: заряда, силы тока и разности потенциалов для незатухающих колебаний.
Решение:
Основой для решения задачи по условию сделаем уравнение:
\[q=A_0e^{\left(-\beta t\right)}{sin \left(\omega t+{\alpha }_0\right)\left(1.1\right).\ }\]Для незатухающих колебаний коэффициент $\beta =0$, тогда уравнение (1.1) примет вид:
\[q=A_0{sin \left({\omega }_0t+{\alpha }_0\right)\left(1.2\right),\ }\]где ${\omega }_0=\sqrt{\frac{1}{LC}}$ -- циклическая частота свободных незатухающих колебаний.
Для того чтобы получить закон изменения силы тока в колебательном контуре используем формулу, связывающую ток и заряд:
\[I=-\frac{dq}{dt}\left(1.3\right),\]где знак минус означает, что положительное направление тока соответствует уменьшению положительного заряда на конденсаторе.
Применим операцию дифференцирования к уравнению (1.2), получим:
\[I=-А_0{\omega }_0{cos \left({\omega }_0t+{\alpha }_0\right)\ }\left(1.4\right).\]Разность потенциалов найдем, используя формулу:
\[\triangle \varphi =\frac{q}{C}=\frac{А_0}{C}{sin \left({\omega }_0t+{\alpha }_0\right).\ }\]Ответ: $q=А_0{sin \left({\omega }_0t+{\alpha }_0\right),\ }I=-А_0{\omega }_0{cos \left({\omega }_0t+{\alpha }_0\right)\ },\ \triangle \varphi =\frac{А_0}{C}{sin \left({\omega }_0t+{\alpha }_0\right).\ }$
Задание: Напишите выражение для периода свободных незатухающих колебаний.
Решение:
За основание для решения задачи возьмем определение периода ($T$) как:
\[T=\frac{2\pi }{{\omega }_0}\left(2.1\right),\]где ${частота\ \omega }_0$- равна:
\[{\omega }_0=\sqrt{\frac{1}{LC}}(2.2)\]Тогда подставив частоту (${\omega }_0)$ из (2.2) в правую часть выражения (2.1), получим известное выражение Томсона:
\[T=2\pi \sqrt{LC}.\]Ответ: $T=2\pi \sqrt{LC}.$












