Допустим, что система состоит из двух контуров, в которых текут токи. Для того чтобы найти энергию магнитного поля этих контуров. необходимо учитывать, что ${{\mathcal E}}_i$ (ЭДС) в каждом из контуров появляется не только за счет изменения потока индукции магнитного поля, которое создается током этого контура, но и за счет изменения потока индукции магнитного поля, которое порождается током в соседнем контуре. Допустим, что: ${{\rm I}}_1$ и ${{\rm I}}_2$ - силы токов в соответствующих контурах, потоки магнитной индукции через первый контур ${\Phi }_{11}$ и ${\Phi }_{12}$ создаются, соответственно, первым и вторым токами. Для второго контура потоки магнитной индукции обозначим как ${\Phi }_{21}$ и ${\Phi }_{22}$. В таком случае полный магнитный поток, который охватывает первый контур (${\Phi }_1$) равен:
суммарный поток через контур (2) равен:
Если $L_{11}$ - индуктивность первого контура, $L_{22}$ - индуктивность второго контура, то можно записать, что:
Поток ${\Phi }_{12}$, который пересекает контур (1), создаваемый током во втором контуре равен:
где $L_{12}$- постоянная, взаимная индуктивность первого и второго контуров. Для второго контура имеем:
Преобразуем формулы (1) и (2) используя выражения для $\ {\Phi }_{11}{,\Phi }_{12},{\Phi }_{21},{\Phi }_{22}$ получим:
Исходя из выражений (6) и (7), ЭДС индукции в первом контуре равна:
ЭДС во втором контуре:
Вся работа, которую совершают источники сторонних ЭДС за время $dt$ может быть представлена выражением:
Далее примем, что:
это будет доказано в примере 2.
Используя равенство (11) имеем:
Следовательно, выражение (10) запишем как:
Проинтегрируем выражение (12), учтем, что сила тока изменяется в контурах от нуля до $I_{1\ }и\ I_2$ соответственно и вся работа идет на магнитную энергию, получим:
Так, мы получили формулу (13), определяющую магнитную энергию, для поля двух контуров с токами.
Обобщим формулу (13) на случай с $N$ контурами:
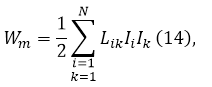
Рисунок 1.
при $i=k$ коэффициент $L_{ik}$ называется индуктивностью контура ${\rm I}$, при $i\ne k$, этот же коэффициент называют взаимной индуктивностью ${\rm I}$-го и $k$-го контуров. Эти коэффициенты определяются формулами при $i\ne k$:
где $d\overrightarrow{l_i},d\overrightarrow{l_k}$ - элементы длины контуров ${\rm I}$-го и k-го. $r_{ik}-$расстояние между ними. При этом $L_{ik}=L_{ki}$.
Задание: Вычислите энергию магнитного поля системы из $N=100$ витков с током, которые намотаны на железный сердечник в виде кольца в один слой. Учесть, что при силе тока ${\rm I}=2 A$ магнитный поток в железе равен $\Phi $=${10}^{-4}Вб.$
Решение:
В качестве основы для решения используем формулу для вычисления магнитной энергии поля, которое создается витками с током. Для случая, который описан в задаче она примет вид:
\[W_m=\frac{LI^2}{2}\left(1.1\right).\]\Psi (потокосцепление), через $N$ витков равно:
\[\Psi =N\Phi \ и\ \Psi =LI\ \left(1.2\right),\]где $\Phi $ - поток магнитной индукции через один виток.
Выразим коэффициент индукции из уравнений (1.2), получим:
\[L=\frac{N\Phi }{I}\left(1.3\right).\]Подставим L из (1.3) в уравнение (1.1), получим:
\[W_m=\frac{\frac{N\Phi }{I}I^2}{2}=\frac{N\Phi I}{2}.\]Все данные в условиях задачи представлены в системе СИ, следовательно, можно провести вычисление магнитной энергии:
\[W_m=\frac{100\cdot 2\cdot {10}^{-4}}{2}={10}^{-2}\left(Дж\right).\]Ответ: $W_m={10}^{-2}Дж.$
Задание: Требуется показать, что взаимные индуктивности системы двух контуров с токами равны, то есть $L_{21}=L_{12}$.
Решение:
Для этого найдем ${\Phi }_{21}и\ {\Phi }_{12}$:
\[{\Phi }_{21}=\int\limits_{S_2}{\overrightarrow{B_1}}d\overrightarrow{S_2},\ {\Phi }_{12}=\int\limits_{S_1}{\overrightarrow{B_2}}d\overrightarrow{S_1}\ \left(2.1\right),\]где $\overrightarrow{B_1}$, $\overrightarrow{B_2}$ - индукции полей, которые созданы токами $I_1\ и\ I_2$. $S_1\ и\ S_2$- поверхности интегрирования, которые натянуты на рассматриваемые контуры. Индукция магнитного поля в каждой точке находится суммированием: $\overrightarrow{B_1}$+$\overrightarrow{B_2}$. Если $\overrightarrow{A_1}$, $\overrightarrow{A_2}$ - векторные потенциалы, соответствующих магнитных полей, то получим:
\[\overrightarrow{B_1}=rot\ \overrightarrow{A_1},\ \overrightarrow{B_2}=rot\ \overrightarrow{A_2},\ \left(2.2\right).\]Тогда выражения (2.1) перепишем в виде:
\[{\Phi }_{21}=\int\limits_{S_2}{rot\ \overrightarrow{A_1}}d\overrightarrow{S_2}=\oint\limits_{L_2}{\overrightarrow{A_1}d\overrightarrow{l_2}},\ {\Phi }_{12}=\int\limits_{S_1}{rot\ \overrightarrow{A_2}}d\overrightarrow{S_1}=\oint\limits_{L_1}{\overrightarrow{A_2}d\overrightarrow{l_1}}\left(2.3\right),\]где $L_1,\ L_2$ - контуры с токами. $d\overrightarrow{l_2}$, $d\overrightarrow{l_1}$ - элементы контуров с токами. Интегральные преобразования выполнены в соответствии с формулой Стокса. Векторный потенциал, для тока можно записать как:
\[\overrightarrow{A_1}=\frac{{\mu }_0}{4\pi }I_1\oint\limits_{L_1}{\frac{d\overrightarrow{l_1}}{r}},\ \overrightarrow{A_2}=\frac{{\mu }_0}{4\pi }I_2\oint\limits_{L_2}{\frac{d\overrightarrow{l_2}}{r}\left(2.4\right).}\]Подставим выражения для векторных потенциалов (2.4) в (2.3), получим:
\[{\Phi }_{21}=\frac{{\mu }_0}{4\pi }I_1\oint\limits_{L_2}{\oint\limits_{L_1}{\frac{d\overrightarrow{l_1}\cdot d\overrightarrow{l_2}}{r_{21}}}},{\Phi }_{12}=\frac{{\mu }_0}{4\pi }I_2\oint\limits_{L_1}{\oint\limits_{L_2}{\frac{d\overrightarrow{l_2}\cdot d\overrightarrow{l_1}}{r_{12}}}}\left(2.5\right),\ \]где $r_{21}=r_{12}$ - расстояния между элементами $d\overrightarrow{l_1}и\ d\overrightarrow{l_2}$. Сравниваем формулу (2.5) с выражениями (4) и (5), получаем:
\[L_{12}=\frac{{\mu }_0}{4\pi }\oint\limits_{L_1}{\oint\limits_{L_2}{\frac{d\overrightarrow{l_2}\cdot d\overrightarrow{l_1}}{r_{12}}}},\ L_{21}=\frac{{\mu }_0}{4\pi }\oint\limits_{L_2}{\oint\limits_{L_1}{\frac{d\overrightarrow{l_1}\cdot d\overrightarrow{l_2}}{r_{21}}}}\left(2.6\right).\]Формула (2.6) показывает, что взаимная индуктивность контуров зависит только от их геометрических характеристик и взаиморасположения. Так как $d\overrightarrow{l_1}и\ d\overrightarrow{l_2}$ - независимые переменные интегрирования можно изменить порядок интегрирования. Используя то, что $r_{21}=r_{12},\ d\overrightarrow{l_2}\cdot d\overrightarrow{l_1}=d\overrightarrow{l_1}\cdot d\overrightarrow{l_2},$ получаем, что:
\[L_{12}=L_{21}\left(2.7\right).\]Что и требовалось доказать.












