Электромагнитная индукция

Определение электромагнитной индукции

Возникновение электрического тока в проводнике, движущемся в магнитном поле, называют явлением индукцией в движущихся проводниках. В случае движения проводника в магнитном поле, его свободные электроны приходят в движение относительно проводника под воздействием силы Лоренца. Явление электромагнитной индукции обнаружил Фарадей в 1831 г. в проводящем контуре. Он заметил, что в замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, которую ограничивает контур, появляется электрический ток. Это также явление электромагнитной индукции, возникающий ток в контуре, называют индукционным.

Итак, явление электромагнитной индукции состоит в возникновении электрического тока в замкнутом проводнике при изменении потока магнитной индукции, охватываемого контуром. При этом контур может быть неподвижным.

ЭДС индукции

Существование явления электромагнитной индукции говорит о том, что при изменении магнитного потока в контуре появляется электродвижущая сила индукции (ЭДС, ${{\mathcal E}}_i$). Величина ${{\mathcal E}}_i$ не зависит от способа изменения магнитного потока $(Ф)$, и связана со скоростью его изменения ($\frac{dФ}{dt}$). С изменением знака скорости изменения потока направление ЭДС индукции тоже изменяется:

Знак потока $Ф$ и знак ${{\mathcal E}}_i$ связывают с выбором направления нормали к плоскости контура. ${{\mathcal E}}_i$ считают положительной если ее направление образует с направлением нормали к контуру правый винт. Для рис 1. и заданном направлении нормали «от нас», перпендикулярно плоскости рисунка ($\overrightarrow{n}$) $\frac{dФ}{dt} >0,\ {{\mathcal E}}_i

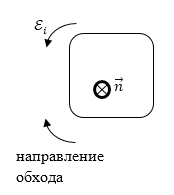
Рисунок 1.

Основной единицей измерения индукционной ЭДС служит вольт $(В)$. Если скорость изменения магнитного потока равна $1\frac{Вб}{с}$ в контуре индуцируется ЭДС, равная $1 В$.

В гауссовой системе формула (1) принимает вид:

где $с$ - скорость света в вакууме. Основной единицей измерения магнитного потока в СГСЭ является максвелл $(Мкс)$, тогда ${{\mathcal E}}_i$ измеряется в СГСЭ - единицах потенциала. Для того, чтобы перевести ЭДС из системы гаусса в вольты необходимо умножить имеющееся значение на $300$. Следовательно, формулой связи системы СИ и СГСЭ можно записать выражение:

Среднее значение ЭДС индукции может быть определено как:

Поток сцепления

Если контур, в котором индуцируется ЭДС, состоит из $N$ витков (соленоид), витки соединены последовательно, ${{\mathcal E}}_i$ равна сумме ЭДС, которые индуцируются каждым витком в отдельности. Следовательно, используя формулу (1), можно записать:

Величину $\Psi$, равную:

называют потоком сцепления, или полным магнитным потоком. В том случае, если поток, который пронизывает каждый из витков, одинаковый, то можно записать, что:

В сложном контуре ${{\mathcal E}}_i$ вычисляют как:

Уравнение (8) называют основным законом электромагнитной индукции (уравнением Фарадея - Максвелла).

Частные случаи применения закона электромагнитной индукции

1. Если проводник длины $l\ $движется в однородном магнитном поле (с индукцией $В$) с постоянной скоростью $v$, то на его концах возникает разность потенциалов $U$:

где $\alpha $ - угол между направлением скорости и вектором магнитной индукции.

1. ЭДС индукции возникает в рамке, которая содержит $N$ витков, имеет площадь $S$ и вращается с постоянной угловой скоростью $\omega$ в однородном магнитном поле с индукцией $В$ и она равна:

где $\omega t$ - мгновенное значение угла между вектором магнитной индукции ($\overrightarrow{B}$) и вектором нормали к плоскости рамки ($\overrightarrow{n}$).