Что такое электромагнитное взаимодействие
Электромагнитным взаимодействием называют взаимодействие между заряженными телами и заряженным телом и электромагнитным полем. Это взаимодействие между заряженными частицами осуществляется через электромагнитное поле.
Электромагнитное взаимодействие относится к фундаментальным взаимодействиям. И стоит в одном ряду с гравитационным, слабым и сильным взаимодействиями. Мир, который нас окружает -- проявление электромагнитного взаимодействия. Большое количество сил в механике имеют электромагнитную природу (силы натяжения, упругости и т.д.). Заряженные частицы являются источниками электромагнитных полей. Частицы, которые не имеют заряда (нейтральные) взаимодействуют с таким полем благодаря сложной внутренней структуре или квантовым эффектам. Это отличает электромагнитное поле от гравитационного, которое действует на все частицы. Но благодаря электромагнитному взаимодействию существуют атомы и молекулы, поскольку их «связывают» электромагнитные силы. Следовательно, электромагнитное взаимодействие -- основа всех существующих явлений на Земле. Химические силы, которые объединяют молекулы из атомов, имеют тоже электромагнитную природу. Сила электромагнитного взаимодействия гораздо больше, чем гравитационного. От слабого и сильного взаимодействия электромагнитное отличает то, что его радиус действия - бесконечность. Способность электромагнитного взаимодействия проявляться на бесконечности объясняется отсутствием у фотона, который является переносчиком данного взаимодействия, массы. Электромагнитное взаимодействие сохраняет свою четность по отношению к пространству, заряду. В этом состоит еще одно отличие электромагнитного взаимодействия от слабого взаимодействия. И электромагнитное взаимодействие не сохраняет изотопический спин -- это отличие от сильного взаимодействия.
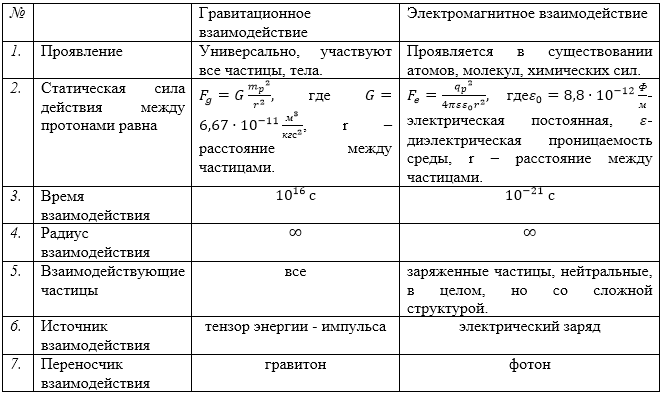
Проведем сравнение гравитационного и электромагнитного взаимодействия по отношению к протону, стабильной частице, которая имеет массу равную $m_p=1,67\cdot {10}^{-27}кг$, заряд протона $q_p=1,6\cdot {10}^{-19}Кл$.
Постоянная электромагнитного взаимодействия
Электромагнитное взаимодействие в микромире характеризуется такой величиной как постоянная электромагнитного взаимодействия $\alpha $, которая определяется как:
\[\alpha =\frac{e^2}{4\pi {\varepsilon }_0\hbar с}\ \left(1\right),\]где $e=-1,6\cdot {10}^{-19}Кл$ -- заряд электрона, $\hbar =\frac{h}{2\pi }=1,05\cdot {10}^{-34}Дж\cdot с$. $с=3•10^8\ \frac{м}{с}$ -- скорость света в вакууме.
Тогда $\alpha \ $равна:
\[\alpha =\frac{{(1,6•{10}^{-19})}^2}{4\cdot 3,14\cdot 8,8•{10}^{-12}\cdot 1,05\cdot {10}^{-34}3\cdot 10^8}\approx \frac{2,56•{10}^{-38}}{348,15•{10}^{-38}}\approx \frac{1}{137}\]Задание: Сравнить силы гравитационного и электростатического взаимодействия между двумя протонами на расстоянии один метр, если частицы находятся в вакууме.
Решение:
Силе гравитационного взаимодействия вычисляется по формуле:
\[F_g=G\frac{{m_p}^2}{r^2}\ (1.1),\]где $G=6,67{\cdot 10}^{-11}\frac{м^3}{кгс^2}$, r -- расстояние между частицами, $m_p=1,67\cdot {10}^{-27}кг$.
Данные в системе СИ, проведем вычисление силы гравитационного притяжения двух протонов ($F_g$):
\[F_g=6,67{•10}^{-11}\frac{{(1,67•{10}^{-27})}^2}{1^2}=18,6\cdot {10}^{-45}\left(Н\right).\]Силу электростатического взаимодействия вычислим по закону Кулона ( в системе СИ):
\[F_e=\frac{{q_p}^2}{4\pi \varepsilon {\varepsilon }_0r^2}\left(1.2\right),\]где${\ \varepsilon }_0=8,8\cdot {10}^{-12}\frac{Ф}{м}$- электрическая постоянная, $\varepsilon $- диэлектрическая проницаемость среды (для вакуума $\varepsilon =1$), $r$ -- расстояние между частицами, заряд протона равен заряду электрона, но со знаком плюс: $q_p=1,6\cdot {10}^{-19}Кл.$
Проведем расчёт:
\[F_e=\frac{{\left(1,6\cdot {10}^{-19}\right)}^2}{4\cdot 3,14\cdot 8,8\cdot {10}^{-12}\cdot 1^2}=\frac{2,56\cdot {10}^{-38}}{110,53\cdot {10}^{-12}}=2,31\cdot {10}^{-28}\ \left(Н\right).\]Ответ: После проведенных вычислений мы получили, что сила гравитационного притяжения между двумя протонами на расстоянии 1 метр будет равна $18,6\cdot {10}^{-45}Н$, а сила электростатического отталкивания между теми же протонами на расстоянии 1 метр будет существенно больше и равна: $2,31\cdot {10}^{-28}\ Н.$
Задание: При каком значении удельного заряда $\frac{q}{m}$ частицы силы гравитационного и электростатического взаимодействия будут равны по модулю, если взаимодействуют две одинаковые частицы?
Решение:
Основой для решения являются закон всемирной гравитации и закон Кулона:
\[F_g=G\frac{m^2}{r^2}\ (2.1),\]где $G$- гравитационная постоянная, $m$ -- массы каждой частицы, $r$ -- расстояние между частицами.
\[F_e=\frac{q^2}{4\pi \varepsilon {\varepsilon }_0r^2}\left(2.2\right),\]где $q$ - заряд каждой частицы, ${\varepsilon }_0$- электрическая постоянная (для системы СИ), $r$ -- расстояние между частицами.
По условию задачи:
\[F_g=F_e\ \left(2.3\right).\]Следовательно:
\[G\frac{m^2}{r^2}=\frac{q^2}{4\pi \varepsilon {\varepsilon }_0r^2}\] \[4\pi \varepsilon {\varepsilon }_0Gm^2=q^2\to \frac{q}{m}=\sqrt{4\pi \varepsilon {\varepsilon }_0G}\left(2.4\right).\]В выражении (2.4) $\varepsilon =1$ (будем считать, что частицы находятся в вакууме), ${\varepsilon }_0=8,8•{10}^{-12}\frac{Ф}{м}$- электрическая постоянная (в системе СИ), $G=6,67{•10}^{-11}\frac{м^3}{кгс^2}$ -- гравитационная постоянная. Подставим имеющиеся данные в уравнение (2.4), найдем искомый удельный заряд:
\[\frac{q}{m}=\sqrt{4\cdot 3,14\cdot 8,8\cdot {10}^{-12}\cdot 6,67{\cdot 10}^{-11}}\approx 8,9{\cdot 10}^{-11}\left(\frac{Кл}{кг}\right).\]Ответ: Удельный заряд частицы (одной из двух одинаковых) должен быть равен $8,9{\cdot 10}^{-11}\frac{Кл}{кг}.$












