Что такое электрический диполь
Электрическим диполем называется система из двух точечных зарядов, величина которых одинакова, но противоположна по знаку, при чем, эти точечные заряды разнесены на небольшое расстояние друг от друга. Вектор, соединяющий отрицательный заряд с положительным (направление от минуса к плюсу), называется плечом диполя.
Тогда векторная величина, равная:
\[\overrightarrow{p_e}=q\overrightarrow{l\ }\left(1\right),\]называется моментом диполя (электрическим моментом диполя). В формуле (1) $q$ -- абсолютное значение каждого из зарядов диполя.
Электрическое поле диполя складывается из напряжённостей зарядов, которые составляют диполь. Так как плечо диполя мало, поэтому можно считать, что оно много меньше, чем расстояние до точек, в которых рассчитывается напряженность поля. Найдем потенциал диполя. В точке А (рис.1) формула для потенциала будет иметь вид:
\[{\varphi }_A=\frac{q}{4\pi {\varepsilon }_0\varepsilon }\left(\frac{1}{r_+}-\frac{1}{r_-}\right)\left(2\right).\]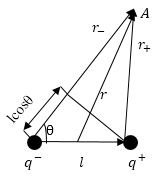
Рис. 1
Так как $l\ll r$, можно считать, что:
\[r_--r_+\approx lcos\theta ,\ r_-\cdot r_+\approx r^2\left(3\right).\]При этом местоположение точки A можно характеризовать вектором$\overrightarrow{\ r}$ с началом в любой точке диполя, ввиду малых геометрических размеров диполя. В таком случае формулу (2) можно записать в виде:
\[\varphi \left(r\right)=\frac{1}{4\pi {\varepsilon }_0\varepsilon }\frac{\overrightarrow{p_e}\cdot \overrightarrow{r}}{r^3}\left(4\right),\]где $qlcos\theta =\frac{\overrightarrow{p_e}\cdot \overrightarrow{r}}{r}.$ Зная связь напряженности поля и потенциала:
\[\overrightarrow{E}=-grad\varphi \ (5)\]запишем формулу для напряженности поля диполя, которая будет иметь вид:
\[\overrightarrow{E}=\frac{1}{4\pi {\varepsilon }_0\varepsilon }\left(\frac{3\left({\overrightarrow{p}}_e\cdot \overrightarrow{r}\right)\overrightarrow{r}}{r^5}-\frac{\overrightarrow{p_e}}{r^3}\right)\left(6\right).\]Согласно формуле (6) напряженность поля диполя убывает быстрее, чем напряженность кулоновского поля одиночного заряда, пропорционально третьей степени расстояния. Силовые линии электростатического поля около диполя изображены на рис. 2.
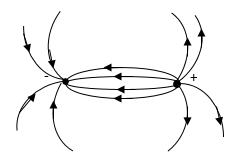
Рис. 2
Модуль вектора сопряженности
Если сферическую систему координат разместить так, чтобы ее центр совпал с серединой плеча диполя, а полярная ось была параллельна $\overrightarrow{p_e}$ (рис.3), то составляющие вектора напряженности будут иметь вид:
\[E_r=\frac{1}{2\pi {\varepsilon }_0\varepsilon }\frac{p_ecos \vartheta}{r^3},E_\vartheta=\frac{1}{4\pi {\varepsilon }_0\varepsilon }\frac{p_esin \vartheta}{r^3},E_{\varphi }=0.\ \left(7\right).\]В таком случае модуль вектора напряженности равен:
\[E=\frac{1}{4\pi {\varepsilon }_0\varepsilon }\frac{p_e}{r^3}\sqrt{3{cos}^2\vartheta+1}\left(8\right).\]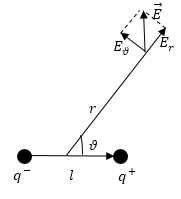
Рис. 3
Вычисление момента сил
В однородном поле сила, которая действует на диполь со стороны поля ($\overrightarrow{F}$), равна нулю, так как к зарядам приложены одинаковые по модулю и противоположные по направлению силы:
\[\overrightarrow{F}={\overrightarrow{F}}_++{\overrightarrow{F}}_-=0\left(9\right),\]где ${\overrightarrow{F}}_+$- сила, действующая на положительный заряд диполя, ${\overrightarrow{F}}$ - сила, действующая на отрицательный заряд диполя.
Момент этих сил равен:
\[\overrightarrow{M}=\overrightarrow{p_e}\times \overrightarrow{E}\left(10\right).\]Момент сил $\overrightarrow{M}$ стремится повернуть ось диполя в направлении поля $\overrightarrow{E}.$ Существует два положения равновесия диполя: диполь параллелен полю (устойчивое положение) и антипараллелен (неустойчивое положение).
Если поле не однородно, то сила (сумма сил действующих на положительный и отрицательный заряд) не равна нулю.$\ \overrightarrow{F}={\overrightarrow{F}}_++{\overrightarrow{F}}_-\ne 0$. В этом случае сила равна:
\[\overrightarrow{F}=q\left({\overrightarrow{E}}_+-{\overrightarrow{E}}_-\right)\left(11\right).\]В том случае, если мы имеем дело с точечным диполем (плечо диполя очень мало), то сила, действующая на диполь, может быть записана как:
\[\overrightarrow{F}=p_{ex}\frac{\partial \overrightarrow{E}}{?x}+p_{ey}\frac{\partial \overrightarrow{E}}{\partial y}+p_{ez}\frac{\partial \overrightarrow{E}}{\partial z}\left(12\right).\]или, что то же самое, но короче:
\[\overrightarrow{F}=\left(\overrightarrow{p}\overrightarrow{\nabla }\right)\overrightarrow{E}\left(13\right).\]Задание: Ответьте на вопрос: может ли точечный заряд двигаться с постоянной скоростью вокруг неподвижного точечного диполя?
Ответ: Может, причем, расстояние заряда от диполя может быть любым. Плоскость круговой орбиты движения точечного заряда будет перпендикулярна оси диполя. Угол между направлением дипольного момента ($\theta $) и радиус -- вектором, который проведен к точечному заряду определяется выражением: cos ($\theta $)=$\pm \sqrt{3}$. Минус относится к положительному заряду.
Задание: Чему равна сила взаимодействия точечного заряда и точечного диполя? Дипольный момент диполя равен $p_e$. Расстояние между зарядом и диполем равно r, дипольный момент направлен вдоль соединяющей их прямой (рис.4).
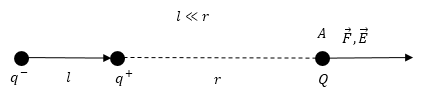
Рис. 4
Напряженность поля, которое создает диполь в точке А (где помещен заряд q) равна:
\[E=q\left(\frac{1}{{r_2}^2}-\frac{1}{{r_1}^2}\right)\left(2.1\right).\]где $r_2$ - расстояние от точки А до положительного конца диполя, $r_1$ -- расстояние до отрицательного конца, но мы считаем диполь точечный (плечо диполя много меньше чем расстояние до точки А ($l\ll r$)), тогда можно (2.1) преобразовать в:
\[E=q\left(\frac{1}{{r_2}^2}-\frac{1}{{r_1}^2}\right)\approx q\frac{d}{dr}\left(\frac{1}{r^2}\right)\left(r_2-r_1\right)={\frac{2ql}{r^3}=\frac{2p_e}{r^3}\left(2.2\right).}\]Тогда силу с которой поле диполя действует на заряд, который помещен в точку А найдем как:
\[F=Q\cdot E\ \left(2.3\right).\]В результате получаем:
\[F=Q\frac{2p_e}{r^3}.\]Ответ: Сила взаимодействия точечного заряда и точечного диполя равна $F=Q\frac{2p_e}{r^3}.$











