Момент импульса
Моментом импульса относительно неподвижной оси $z$ называется скалярная величина $L_{z} $, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси.
Значение момента импульса $L_{z} $ не зависит от положения точки 0 на оси $z$. При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдельная точка тела движется по окружности постоянного радиуса $r_{i} $ с некоторой скоростью $v_{i} $. Скорость $v_{i} $ и импульс $m_{i} v_{i} $ перпендикулярны этому радиусу, т.е. радиус является плечом вектора $m_{i} v_{i} $. Поэтому можно записать, что момент импульса отдельной точки относительно оси $z$ равен:
\[L_{iz} =m_{i} v_{i} r_{i} .\]Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его точек:
\[L_{z} =\sum \limits _{i=1}^{n}m_{i} v_{i} r_{i} \]Учитывая связь между линейно и угловой скоростями ($v_{i} =\omega r_{i} $), получим следующее выражение для момента импульса тела относительно неподвижной оси:
$L_{z} =\sum _{i=1}^{n}m_{i} r_{i}^{2} \omega =\omega \sum \limits _{i=1}^{n}m_{i} r_{i}^{2} =J_{z} \omega $, (1)
т.е. момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость. Продифференцировав выражение (1) по времени, получим:
$\frac{dL_{z} }{dt} =J_{z} \frac{d\omega }{dt} =M_{z} $ (2)
Это еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всех внешних сил, действующих на тело.
Закон сохранения импульса
Закон сохранения момента импульса вытекает из основного уравнения динамики вращательного движения тела, закрепленного в неподвижной точке, и состоит в следующем: если результирующий момент внешних сил относительно неподвижной точки тождественно равен нулю, то момент импульса тела относительно этой точки с течением времени не изменяется.
Действительно, если:
$M=0$, то $\frac{dL}{dt} =0$,
откуда: $\overline{L}=const$. (3)
Другими словами, момент импульса замкнутой системы с течением времени не изменяется.
Из основного закона динамики тела, вращающегося вокруг неподвижной оси $z$ (уравнение 2), следует закон сохранения момента импульса тела относительно оси: если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется в процессе движения, т.е. если $M_{z} =0$, то $\frac{dL_{z} }{dt} =0$, откуда $\overline{L}_{z} =const,$ или $J_{z} \omega =const$.(4)
Закон сохранения момента импульса является фундаментальным законом природы. Справедливость этого закона обусловливается свойством симметрии пространства -- его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета.
Справедливы следующие выражения:
- Момент инерции тела относительно оси вращения -- это физическая величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний до рассматриваемой оси: \[J_{z} =\sum \limits _{i=1}^{n}m_{i} r_{i}^{2} ;\]
- Момент инерции тела $J_{z} $ относительно любой оси вращения равен моменту его инерции $J_{c} $относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями: $J_{z} =J_{c} +ma^{2} $;
- При вращении абсолютно твердого тела вокруг неподвижной оси $z$ его кинетическая энергия равна половине произведения момента инерции относительно оси вращения на квадрат угловой скорости: \[E_{k_{2@} } =\frac{J_{z} \omega ^{2} }{2} ;\]
- Из сравнения формул $E_{k_{2@} } =\frac{J_{z} \omega ^{2} }{2} $и $E_{k} =\frac{mv^{2} }{2} $ следует, что момент инерции -- мера инертности тела при вращательном движении;
- Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z (аналог второго закона Ньютона) имеет вид: $M_{z} =J_{z} \varepsilon =\frac{dL_{z} }{dt} $.
Груз массой 0,8 кг подвешен на тонкой невесомой нити, на высоте 3 м над полом. Нить намотана на сплошной однородный цилиндрический вал радиусом 30 см с моментом инерции 0,15 кг*м2. Вращаясь, вал опускает груз на пол. Определить: время опускания груза до пола, силу натяжения нити, кинетическую энергию груза в момент касания грузом пола.
Дано:
$r$= 15 см=0,15м
$J_{x} $= 0,18 кг*м2
$m$= 0,5 кг
$h$=3 м
Найти: $t,N,E_{k} $-?
Решение:
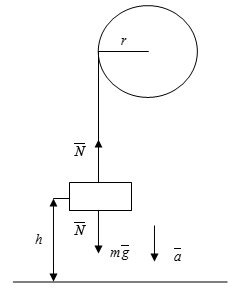
Запишем закон сохранения энергии для нашей системы:
$mgh=\frac{mv^{2} }{2} +\frac{J_{x} \omega ^{2} }{2} $ (1)
Записав формулы для пути, линейной и угловой скоростей и подставив в уравнение (1), получим:
\[ \omega =\frac{v}{r} ; h=\frac{at^{2} }{2} ; v=at;\] \[mg\frac{at^{2} }{2} =\frac{at^{2} }{2} (m+\frac{J_{x} }{r^{2} } ).\]Тогда: $a=\frac {mg}{m+ \frac {J_x}{r^2} } = \frac {0,5 \cdot 10}{0,5+\frac{0,18}{0,15^2 } } \approx 0,6 м/с^2$
и искомое время опускания: $t=\sqrt{\frac{2h}{a} } =\sqrt{\frac{2\cdot 3}{0,6} } \approx 3,2c.$
Уравнение динамики вращательного движения вала:
\[Nr=J_{x} \varepsilon ;\]где $\varepsilon =\frac{a}{r} $- угловое ускорение вала;
Отсюда, сила натяжения нити: $N=\frac{J_{x} \varepsilon }{r} =\frac{0,18\cdot 4}{0,15} =4,8H$.
Кинетическая энергия груза в момент удара об пол:
\[E_{k} =\frac{mv^{2} }{2} =\frac{ma^{2} t^{2} }{2} =\frac{0,5\cdot 0,6^{2} \cdot 3,2^{2} }{2} \approx 0,9Дж.\]Ответ: $t=3,2A$, $N=4,8H$, $E_{k} =0,9Дж.$











