Приведенная масса
Решение уравнений динамики системы материальных точек встречает непреодолимые математические трудности, т.к. точного решения этих уравнений для произвольных сил не найдено уже в случае трех материальных точек.
В связи с этим важна задача о замкнутой системе двух точек, называемая задачей двух тел. Она имеет простое и исчерпывающее решение -- сводится к основной задаче динамики одной материальной точки. Решение задачи двух тел используется в небесной механике, описывающей движение планет и их спутников в Солнечной системе, в задачах на столкновение частиц, в статистической физике и других вопросах.
Рассмотрим замкнутую систему двух материальных точек, взаимодействующих между собой. Как известно центр масс такой системы движется равномерно и прямолинейно (или покоится). Задача просто решается в системе с началом в центре масс, движущейся поступательно (такая система называется Ц-системой).
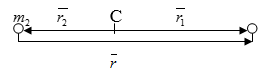
Рисунок 1.
Обозначим массы частиц через $m_{1} $ и $m_{2} $ и их радиус-векторы, проведенные от центра масс, соответственно $\overline{r_{1} }$ и $\overline{r_{2} }$. Пусть $\overline{r}$- вектор, проведенный от точки $m_{2} $ к $m_{1} $. Из определения радиус-вектора центра масс имеем:
Непосредственно из рисунка следует соотношение между радиус-векторами:
$\overline{r}_{1} =\overline{r}_{2} +\overline{r}$. (1)
Два последних равенства позволяют выразить радиус-векторы $\overline{r_{1} }$ и $\overline{r_{2} }$ через вектор $\overline{r}$, соединяющий точки $m_{2} $ и $m_{1} $. Имеем:
$\overline{r}_{1} =\frac{m_{2} }{m_{1} +m_{2} } \overline{r}$, $\overline{r}_{2} =\frac{m_{1} }{m_{1} +m_{2} } \overline{r}$. (2)
Запишем основные уравнения для движения обеих точек в Ц-системе:
$\begin{array}{l} {m_{1} \overline{\ddot{r}_{1} }=\overline{F}_{2,1} (r)} \\ {m_{2} \overline{\ddot{r}_{2} }=\overline{F}_{1,2} (r)} \end{array}$ (3)
Силы в уравнениях (3) зависят от расстояния между точками, а не от расстояния до центра масс, т.е. решать уравнения (1) отдельно для каждой точки нельзя.
Пользуясь выражениями для радиус-векторов (2), исключим из основных уравнений (3) $\overline{r_{1} }$ и $\overline{r_{2} }$. Тогда получаем уравнения движения:
Так как по третьему закону Ньютона $\overline{F}_{2,1} (r)=-\overline{F}_{1,2} (r)$, оба уравнения становятся тождественными, и движение системы двух точек, в результате их взаимодействия эквивалентно движению одной точки в соответствии с уравнением:
$\frac{m_{1} B_{2} }{m_{1} +m_{2} } \overline{\ddot{r}}=\overline{F}(r)$. (4)
Уравнение (4) отличается от известного уравнения движения материальной точки в поле заданной силы только тем, что вместо массы $m$здесь выступает комбинация масс двух точек:
$m'=\frac{m_{1} B_{2} }{m_{1} +m_{2} } $ (5)
Величина $m'$ называется приведенной массой.
Итак, задача двух тел свелась к задаче о движении одной материальной точки с приведенной массой в Ц-системе под действием центральной силы; уравнение движения имеет обычный вид:
$m'\overline{\ddot{r}}=\overline{F}(r)$ (6)
Но при использовании результатов решения уравнения (6) необходимо помнить, что точка $m'$, движущаяся на конце радиус-вектора $\overline{r}$под действием силового центра в начале координат Ц-системы, является не реальной, а изображающей движение системы. От ее движения, после того как уравнение (6) проинтегрировано, следует переходить к реальному движению двух материальных точек $m_{2} $ и $m_{1} $.
Движение двух материальных точек в системе центра масс
Движение изображающей точки в соответствии с уравнением (6) будет плоским. Пусть кинематическое уравнение движения найдено: $\overline{r}=\overline{r}(t)$.
В таком случае с помощью формулы (2) находим кинематическое уравнение движения обеих материальных точек в Ц-системе:
$\overline{r}_{1} =\frac{m_{2} }{m_{1} +m_{2} } \overline{r}(t),$ $\overline{r}_{2} =\frac{m_{1} }{m_{1} +m_{2} } \overline{r}(t)$. (7)
Очевидно, что траектория движения изображающей точки и точек $m_{2} $ и $m_{1} $ будут подобными кривыми относительно центра масс, а отношение подобия есть обратное отношение масс, т.е.:
$\frac{r_{1} }{r_{2} } =\frac{m_{2} }{m_{1} } $ (8)
Нетрудно найти и скорости движения точек. Дифференцируя (7) по времени, имеем:
$\overline{v}_{1} =\frac{m_{2} }{m_{1} +m_{2} } \overline{v},$ $\overline{v}_{2} =\frac{m_{1} }{m_{1} +m_{2} } \overline{v}$. (9)
Задача двух тел решена.
Момент импульса для системы двух точек имеет вид: $\overline{L}=m_{1} \left|\overline{r}_{1} \overline{v}_{1} \right|+m_{2} \left|\overline{r}_{2} \overline{v}_{2} \right|$. Необходимо записать выражение для собственного момента импульса системы через приведенную массу.
Дано:
Момент импульса системы двух точек: $\overline{L}=m_{1} \left|\overline{r}_{1} \overline{v}_{1} \right|+m_{2} \left|\overline{r}_{2} \overline{v}_{2} \right|$.
Найти: собственный момент импульса системы - ?
Момент импульса системы двух точек:
\[\overline{L}=m_{1} \left|\overline{r}_{1} \overline{v}_{1} \right|+m_{2} \left|\overline{r}_{2} \overline{v}_{2} \right|.\]Внесем сюда выражения $\overline{r_{1} }$ и $\overline{r_{2} }$через вектор $\overline{r}$, выражающийся формулой (7) и получим равенство:
\[\overline{L}=\frac{m_{1} m_{2} }{m_{1} +m_{2} } \left|\overline{r}\overline{v}_{1} \right|-\frac{m_{1} m_{2} }{m_{1} +m_{2} } \left|\overline{r}\overline{v}_{2} \right|=\frac{m_{1} m_{2} }{m_{1} +m_{2} } (\overline{r}\left|\overline{v}_{1} -\overline{v}_{2} \right|).\]Вектор $\overline{v}_{1} -\overline{v}_{2} $ есть скорость $\overline{v'}$первой частицы относительно второй или скорость изображающей точки $\overline{v}$ и окончательный результат выражается равенством:
\[\overline{L}=m'[\overline{r}\overline{\cdot v}].\]Ответ: собственный момент импульса системы $\overline{L}=m'[\overline{r}\overline{\cdot v}]$
Выводы:
-
задача о движении двух тел сводится к задаче о движении одной точки под действием заданной силы;
-
особую роль при этом играет приведенная масса системы, через нее выражаются основные динамические параметры системы -- энергия, импульс, момент импульса.











