Орбиты небесных тел
Орбиты небесных тел - траектории, по которым движутся в космическом пространстве Солнце, звезды, планеты, кометы, а также искусственные космические аппараты (искусственные спутники Земли, Луны и других планет, межпланетные станции и т. п.). Однако для искусственных космических аппаратов термин «орбита» применяют лишь к тем участкам их траекторий, на которых они движутся с выключенной двигательной установкой (так называемые пассивные участки траектории).
Формы орбит и скорости, с которыми движутся по ним небесные тела, определяются главным образом силой всемирного тяготения. При исследовании движения небесных тел в большинстве случаев допустимо не принимать во внимание их форму и строение, т. е. считать их материальными точками. Такое упрощение возможно потому, что расстояние между телами обычно во много раз больше их размеров. Считая небесные тела материальными точками, мы можем при исследовании их движения непосредственно применять закон~всемирного тяготения. Кроме того, во многих случаях можно ограничиться рассмотрением движения только двух притягивающихся тел, пренебрегая влиянием других. Так, например, при изучении движения планеты вокруг Солнца можно с известной точностью предполагать, что планета движется только под действием сил солнечного тяготения. Точно так же при приближенном изучении движения искусственного спутника планеты можно принять во внимание лишь тяготение «своей» планеты, пренебрегая не только притяжением других планет, но и солнечным.
Указанные упрощения приводят к так называемой задаче двух тел. Одно из решений этой задачи было дано И. Кеплером, полное решение задачи было получено И. Ньютоном. Ньютон доказал, что одна из притягивающихся материальных точек обращается вокруг другой по орбите, имеющей форму эллипса (или окружности, которая является частным случаем эллипса), параболы или гиперболы. В фокусе этой кривой находится вторая точка.
Форма орбиты зависит:
- от масс рассматриваемых тел;
- от расстояния между ними;
- от скорости, с которой одно тело движется относительно другого.
Если тело массой $m_{1} $(кг) находится на расстоянии $r$ (м) от тела массой $m_{0} $ (кг) и движется в этот момент времени со скоростью $v$ (м/с), то вид орбиты определяется величиной:
Постоянная тяготения $f=6.673\cdot 10^{-11} \ м^3 \ кг^{-1} \ c^{-2}$. Если $h0$ - по гиперболической орбите.
Наименьшая начальная скорость, которую нужно сообщить телу, чтобы оно, начав движение вблизи поверхности Земли, преодолело земное притяжение и навсегда покинуло Землю по параболической орбите, называется второй космической скоростью. Она равна $11,2$ км/с. Наименьшая начальная скорость, которую нужно сообщить телу, чтобы оно стало искусственным спутником Земли, называется первой космической скоростью. Она равна $7,91$ км/с.
По эллиптическим орбитам движется большинство тел Солнечной системы. Только некоторые малые тела Солнечной системы - кометы, возможно, движутся по параболическим или гиперболическим орбитам. В задачах космического полета наиболее часто встречаются эллиптические и гиперболические орбиты. Так, межпланетные станции отправляются в полет, имея гиперболическую орбиту относительно Земли; затем они движутся по эллиптическим орбитам относительно Солнца по направлению к планете назначения.
Характеристики движения небесных тел
Ориентация орбиты в пространстве, ее размеры и форма, а также положение небесного тела на орбите определяются шестью величинами, называемыми элементами орбиты. Некоторые характерные точки орбит небесных светил имеют собственные названия. Так, ближайшая к Солнцу точка орбиты небесного тела, движущегося вокруг Солнца, называется перигелием, а наиболее удаленная от него точка эллиптической орбиты - афелием. Если рассматривается движение тела относительно Земли, то ближайшая к Земле точка орбиты называется перигеем, а самая далекая - апогеем. В более общих задачах, когда под притягивающим центром можно подразумевать разные небесные тела, употребляют названия: перицентр (ближайшая к центру точка орбиты) и апоцентр (наиболее удаленная от центра точка орбиты).
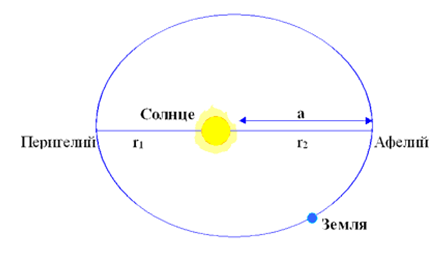
Рисунок 1.
Случай взаимодействия только двух небесных тел является простейшим и почти не наблюдается (хотя и имеется много случаев, когда притяжением третьего, четвертого и т. д. тел можно пренебречь). В действительности все обстоит намного сложнее: на каждое тело действуют многие силы. Планеты в своем движении притягиваются не только к Солнцу, но и друг к другу. В звездных скоплениях каждая звезда притягивается всеми остальными. На движение~искусственных спутников Земли оказывают влияние силы, вызываемые несферичностью фигуры Земли и сопротивлением земной атмосферы, притяжение Луны и Солнца. Эти дополнительные силы называют возмущающими, а эффекты, которые они вызывают в движении небесных тел, - возмущениями. Из-за возмущений орбиты небесных тел непрерывно медленно изменяются.
Исследованием движения небесных тел с учетом возмущающих сил занимается раздел астрономии - небесная механика. Методы, разработанные в небесной механике, позволяют очень точно на много лет вперед определить положение любых тел Солнечной системы. Более сложные методы вычислений используются при исследовании движения искусственных небесных тел. Точное решение этих задач в аналитическом виде (т. е. в виде формул) получить крайне сложно. Поэтому используются методы численного решения уравнений движения с применением быстродействующих электронных вычислительных машин. При таких вычислениях пользуются понятием сферы действия планеты.
Сферой действия называют область околопланетного (или окололунного) пространства, в которой при расчетах возмущенного движения тела (межпланетного космического корабля, спутника планеты, кометы) удобно в качестве центрального тела считать не Солнце, а эту планету (или Луну). В этом случае расчеты упрощаются вследствие того, что внутри сферы действия возмущающее влияние притяжения Солнца в сравнении с притяжением планеты меньше, чем возмущение от планеты в сравнении с притяжением Солнца. Но нужно помнить, что и внутри сферы действия и за ее пределами - всюду на тело действуют силы притяжения и Солнца, и планеты, и других тел, хотя и в разной степени.
Радиус сферы действия зависит от расстояния между Солнцем и планетой. Орбиты небесных тел внутри сферы действия можно рассчитывать на основе задачи двух тел. Если небесное тело покидает планету, то движение этого тела внутри сферы действия происходит по гиперболической орбите. Радиус сферы действия Земли равен около $1$ млн. км; сфера действия Луны по отношению к Земле имеет радиус около $63$ тыс. км.
Метод определения орбиты небесного тела с использованием понятия сферы действия - один из способов приближенного определения орбит. Зная приближенные величины элементов орбиты, можно с помощью других методов получить более точные значения элементов орбиты. Такое поэтапное улучшение определяемой орбиты является типичным приемом, позволяющим вычислить параметры орбиты с высокой точностью. В настоящее время круг задач по определению орбит значительно расширился, что объясняется бурным развитием ракетной и космической техники.
Определите, во сколько раз масса Сщлнца больше массы Земли, если известно, что период обращения Луны вокруг Земли $27,2$ сут., а среднее расстояние ее от Земли $384000$ км.
Дано: $T_{;} =27,2$сут., $a_{;} =3.84\cdot 10^{5} $км.
Найти: $\frac{m_{c} }{m_{3} } $-?
Решение: Указанные выше упрощения приводят нас к так называемой задаче двух тел. Одно из решений этой задачи было дано И. Кеплером, полное решение задачи было получено И. Ньютоном. Воспользуемся этими решениями.
$T_{3} =365$сут -- период обращения Земли вокруг Солнца
$a_{3} =1.5\cdot 10^{8} $км -- среднее расстояние от Земли до Солнца.
Для решения используем формулу третьего закона Кеплера с учетом второго закона Ньютона:
\[\frac{m_{c} +m_{3} }{m_{3} +m_{;} } \cdot \frac{T_{3}^{2} }{T_{;}^{2} } =\frac{a_{3}^{3} }{a_{;}^{3} } .\]Учитывая, что масса Земли по отношению к массе Солнца и масса Луны по отношению к массе Земли ничтожно малы, то формулу можно переписать в виде:
\[\frac{m_{c} }{m_{3} } \cdot \frac{T_{3}^{2} }{T_{;}^{2} } =\frac{a_{3}^{3} }{a_{;}^{3} } \]Отсюда находим искомое отношение масс:
\[\frac{m_{c} }{m_{3} } =\frac{a_{3}^{3} }{a_{;}^{3} } \cdot \frac{T_{3}^{2} }{T_{;}^{2} } .\]Ответ: $\frac{m_{c} }{m_{3} } =0,3\cdot 10^{6} $.











