Первая космическая скорость
Чтобы понять, при каких условиях тело может стать искусственным спутников Земли, рассмотрим рисунок 1. Он представляет собой копию рисунка, сделанного Ньютоном. На этом рисунке изображен земной шар, а на нем показана высокая гора, с вершины которой бросают камни, придавая им различные по модулю и горизонтально направленные скорости. Брошенные камни отклоняться под действием силы тяжести от прямолинейного пути и, описав кривую траекторию, упадет, наконец, на Землю.
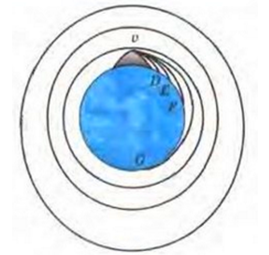
Рисунок 1.
Если бросить камень с большей скоростью, то он упадет дальше.
Таким образом, при отсутствии сопротивления воздуха и при достаточно большой скорости тело вообще может не упасть на Землю, а будет описывать круговые траектории, оставаясь на одной и той же высоте над Землей.
Для того чтобы двигаться вокруг Земли по круговой орбите с радиусом, мало отличающимся от радиуса Земли $R_{3} $, тело должно обладать вполне определенной скоростью $v_{1} $, величину которой можно определить из условия равенства произведения массы тела на ускорение силы тяжести, действующей на тело:
Отсюда:
Следовательно, для того чтобы какое-либо тело стало спутником Земли, ему необходимо сообщить скорость $v_{1} $ которая называется первой космической скоростью. Подстановка значений $g$ и $R_{3} $ дает для первой космической скорости следующее значение:
$v_{1} =\sqrt{gR_{3} } =8$км/с.
Вторая космическая скорость
Обладая скоростью $v_{1} $, тело не упадет на Землю. Однако этой скорости недостаточно для того, чтобы тело могло выйти из сферы земного притяжения, т. е. удалиться от Земли на такое расстояние, что притяжение к Земле перестает играть существенную роль. Необходимая для этого скорость $v_{x} $ называется второй космической скоростью.
Для того чтобы найти вторую космическую скорость, нужно вычислить работу, которую необходимо совершить против сил земного притяжения для удаления тела с поверхности Земли на бесконечность. При удалении тела силы земного притяжения совершают над ним работу:
Начальное значение равно:
Конечное значение есть нуль. Таким образом:
Работа $A$, которую нужно совершить против сил земного притяжения, равна работе $A'$, взятой с обратным знаком, т. е.:
Пренебрегая различием между силой тяжести $mg$ и силой гравитационного притяжения тела к Земле, можно написать, что:
Отсюда:
Следовательно, работу можно представить в виде:
Эту работу удаляющееся тело совершает за счет запаса своей кинетической энергии. Чтобы запас энергии оказался достаточным для совершения работы, тело должно быть запущено со скоростью, не меньшей, чем скорость $v_{1} $, определяемая условием:
Отсюда:
Скорость $v_{2} $ и есть вторая космическая скорость. Из сравнения видно, что вторая космическая скорость в $\sqrt{2} $ раз больше первой. Умножив $8$ км/с на $\sqrt{2} $, получим для $v_{2} $ значение, приблизительно равное $11$ км/с.
Отметим, что необходимая величина скорости не зависит от направления, в котором осуществляется запуск тела с Земли. От этого направления зависит лишь вид траектории, по которой тело удаляется от Земли.
Третья космическая скорость
Для того чтобы покинуть пределы Солнечной системы, тело должно преодолеть, кроме сил притяжения к Земле, также и силы притяжения к Солнцу. Необходимая для этого скорость запуска тела с поверхности Земли называется третьей космической скоростью} $v_{3} $.
Скорость $v_{3} $ зависит от направления запуска. При запуске в направлении орбитального движения Земли эта скорость минимальна и составляет около $17$ км/с (в этом случае скорость тела относительно Солнца складывается из скорости тела относительно Земли и скорости, с которой Земля движется вокруг Солнца). При запуске в направлении, противоположном направлению движения Земли, $v_{3} \approx 73$км/с.
Впервые космические скорости были достигнуты в СССР. $4$ октября $1957$ г. в Советском Союзе был осуществлен первый в истории человечества успешный запуск искусственного спутника Земли. $2$ января $1959$ г. был взят и второй рубеж. В этот день с советской земли отправилась в полет космическая ракета, которая вышла из сферы земного притяжения и стала первой искусственной планетой нашей Солнечной системы. $12$ апреля $1961$ г. в Советском Союзе был осуществлен первый полет человека в космическое пространство. Первый советский космонавт Юрий Алексеевич Гагарин совершил полет вокруг Земли и благополучно приземлился.
Определите первую космическую скорость для спутника Юпитера, летающего на небольшой высоте, если масса планеты $1,9\cdot 10^{27} $ кг, а радиус $R=7,13\cdot 10^{7} $ м.
Дано: $B=1,9\cdot 10^{27} $ кг, $R=7,13\cdot 10^{7} $ м.
Найти: $v_{1} $-?
Решение: Запишем формулу для нахождения первой космической скорости:
$v_{1} =\sqrt{gR_{3} } $, (1)
$g$ - ускорение свободного падения на Юпитере.
Записав закон всемирного тяготения для нашего случая, имеем:
$mg=G\frac{Mm}{r^{2} } $, (2)
где $m$- масса спутника, $M$ - масса Юпитера,
Если высота спутника над поверхностью Юпитера мала по сравнению с его радиусом, то ее можно пренебречь и считать:
\[r=R.\]Тогда из уравнения (2) можем найти ускорение свободного падения для Юпитера:
\[g=G\frac{M}{R^{2} } .\]Подставив выражение для ускорения в уравнение (1), найдем искомую первую космическую скорость:
$v_{1} =\sqrt{G\frac{M}{R} } =42159,45$м/с.
Ответ: $v_{1} =42159,45$ м/с.











