Дифференциальные уравнения движения системы
Рассмотрим систему, состоящую из $n$ материальных точек. Выделим какую-нибудь точку системы с массой $m_{k}.$ Обозначим равнодействующую всех приложенных к точке внешних сил (и активных, и реакций связей) через $\overline{F}_{k}^{e} $, а равнодействующую всех внутренних сил -- через $\overline{F}_{k}^{l} $. Если точка имеет при этом ускорение $\overline{a_{k} }$, то по основному закону динамики:
Аналогичный результат получим для любой точки. Следовательно, для всей системы будет:
Уравнения (1) представляют собой дифференциальные уравнения движения системы в векторной форме.
Проектируя равенства (1) на координатные оси, получим уравнения движения системы в дифференциальной форме в проекциях на эти оси.
Однако при решении многих конкретных задач необходимость находить закон движения каждой из точек системы не возникает, а бывает достаточно найти характеристики, определяющие движение всей системы в целом.
Теорема о движении центра масс системы
Для определения характера движения системы требуется знать закон движения ее центра масс. Центром масс или центром инерции системы называется такая воображаемая точка, радиус-вектор $R$которой выражается через радиус векторы $r_{1} ,r_{2} ,...$материальных точек по формуле:
$R=\frac{m_{1} r_{1} +m_{2} r_{2} +...+m_{n} r_{n} }{m} $, (2)
где $m=m_{1} +m_{2} +...+m_{n} $ - общая масса всей системы.
Чтобы найти этот закон, обратимся к уравнениям движения системы (1) и сложим почленно их левые и правые части. Тогда получим:
$\sum m_{k} \overline{a}_{k} =\sum \overline{F}_{k}^{e} +\sum \overline{F}_{k}^{l} $. (3)
Из формулы (2) имеем:
Беря вторую производную по времени, получаем:
$\sum m_{k} \overline{a}_{k} =M\overline{a}_{c} $, (4)
где $\overline{a}_{c} $- ускорение центра масс системы.
Так как по свойству внутренних сил в системе $\sum \overline{F}_{k}^{l} =0$, получим окончательно из равенства (3), учтя (4):
$M\overline{a}_{c} =\sum \overline{F}_{k}^{e} $. (5)
Уравнение (5) выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил или центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.
Проецируя обе части равенства (5) на координатные оси, получим:
$M\ddot{x}_{c} =\sum \overline{F}_{kx}^{e} $, $M\ddot{y}_{c} =\sum \overline{F}_{ky}^{e} $, $M\ddot{z}_{c} =\sum \overline{F}_{kz}^{e} $. (6)
Эти уравнения представляют собой дифференциальные уравнения движения центра масс в проекциях на оси декартовой системы координат.
Значение теоремы состоит в следующем:
- Поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе тела. В остальных случаях тело можно рассматривать как материальную точку лишь тогда, когда практически для определения положения тела достаточно знать положение его центра масс и допустимо по условиям задачи не принимать во внимание вращательную часть движения тела;
- Теорема позволяет исключать из рассмотрения все наперед неизвестные внутренние силы. В этом ее практическая ценность.
Металлическое кольцо, подвешенное на нити к оси центробежной машины равномерно вращается с угловой скоростью $\omega $. Нить составляет угол $\alpha $с осью. Найти расстояние от центра кольца до оси вращения.
Дано:
\[\omega \] \[\alpha \]Найти:
$R$-?
Решение:
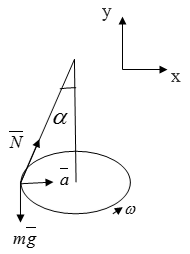
На нашу систему действует сила тяжести $\overline{N}$ $\overline{N}$ $\alpha \alpha$, сила натяжения нити и центростремительное ускорение.
Запишем второй закон Ньютона для нашей системы:
\[m\overline{a}=\overline{N}+m\overline{g}\]Спроецируем обе части на оси x и y:
\[\left\{ \begin{array}{c} N\sin \alpha =ma; \\ N\cos \alpha =mg; \end{array} \right.(4)\]Разделив одно уравнение на другое, получим:
\[tg\alpha =\frac{a}{g} .\]Так как $a=\frac{v^{2} }{R} ;$$v=\omega R$, находим искомое расстояние:
\[R=\frac{gtg\alpha }{\omega ^{2} } \]Ответ: $R=\frac{gtg\alpha }{\omega ^{2} } $











