Решение уравнения Шредингера для молекул очень сложно с математической точки зрения. Поэтому при расчетах молекул часто используются различные приближенные методы. Вкратце остановимся на 2-х основных методах расчета молекул:метод валентных сязей и метод молекулярных орбиталей.
Теория молекулярных орбиталей, как мы видели, является естественным распространением на молекулы тех идей, которые сначала были использованы для объяснения электронного строения атомов. Однако молекулярно-орбитальная теория строения исторически не была первой; она просто очень быстро развилась из-за того, что ее легче приспособить для расчетов на компьютерах, чем другие теории. Исторически первой была теория валентных связей, которая используется и в настоящее время.
Метод валентных связей (МВС)
Метод валентных связей ($BC$) исторически является первым квантово-химическим методом: именно в его рамках Гайтлер и Лондон рассчитали в 1927 г. молекулу водорода. В этом методе учитывают, что атомы в молекулах сохраняют во многом свою индивидуальность, а эффект химической связи рассматривается как возмущение, приводящее к обмену электронами и их спариванию в соответствии с требованием принципа Паули. Поэтому многоэлектронная волновая функция $Y$ строится как линейная комбинация линейно-независимых антисимметризованных произведений наборов $AO$ со спиновыми частями, выбранными по специальным правилам:
$\Psi = \Upsilon C_i \Psi i^{BC}$ (1)
Каждая функция $Y$ $i$ $BC$ соответствует набору атомов в определенных электронных конфигурациях и называется валентной структурой ($BC$). Параметры орбиталей в $BC$ и их веса $ci$ определяются с помощью вариационного принципа. Электронное строение и свойства системы, таким образом, представляются в методе $BC$ как среднее по различным $BC$, число которых может быть очень велико (иногда, впрочем, для хорошего описания достаточно несколько $BC$).
$NBC$ основан на предположении, что ковалентная химическая связь характеризуется перекрыванием валентных орбиталей атомов, участвующих в химической связи. Например, химическая связь атомов $A$ и $B$, образованная парой электронов в $1s$ состоянии с антипараллельными спинами характеризуется областью перекрывания двух окружностей, которые изображают орбитали электронов, принадлежащих ядрам $a$ и $b$ .
Величина области перекрывания характеризует силу связи. Другими словами идея этого метода состоит в том, что в каждой молекуле химические связи двухэлектронные, двухцентровые и локализованные.
Эта схема химической связи реализована в молекуле $H_{2} $, где химическая связь создается двумя электронами, находящимися на $1s$ орбиталях атомов водорода, т.е. имеет место перекрывание орбиталей $s-s$.
В случае образования химической связи электронами $p$-типа, степень перекрывания электронных облаков зависит не только от расстояния между ядрами, но и от направления, по которому происходит их сближение. Ориентация атомных орбиталей должна быть такой чтобы достигалось максимальное перекрывание орбиталей, участвующих в химической связи, и минимальное перекрывание остальных орбиталей. При такой схеме, связи всегда ориентированы относительно друг друга под определенными валентными углами. Эта идея впервые была сформулирована Полингом и носит название принципа максимального перекрывания.
Рассмотрение некоторых видов химических связей
Химические связи имеют то общее свойство, что электронное облако, описывающее вероятностное распределение двух электронов, участвующих в образовании ковалентной связи, симметрично относительно вращения вокруг линии связи. Такого типа связи называются $\sigma $ - связями.
Существует другой тип перекрывания волновых функций $p$-электронов, который приводит к так называемой $\pi $-связи.
$\pi $-связи возникают в случае кратных связей т.е. когда между 2-мя атомами насыщаются 2 или 3 связи.
Например, в молекулах этилена $C_{2} H_{4} $ и ацетилена $C_{2} H_{2} $.
Используя метод двухцентровых связей, можно построить для рассматриваемой молекулы множество структурных схем, которые называются предельными структурами данной молекулы. Для нахождения предельных структур существует правило Рюмера, согласно которому $2n$ орбиталей образуют двухэлектронные связи. $2n$ - число электронов молекулы, образующих $\pi $- связь.
Символы молекулы располагаются по кругу (независимо от формы молекулы), соединяются попарно линиями, так чтобы они не пересекались. Эти структуры являются независимыми. Число структурных схем определяется по формуле:
$\frac{\left(2n\right)!}{n!\left(n+1\right)!} $ (2)
Для каждой структуры находят волновую функцию молекулы. Полная волновая функция молекулы берется как линейная комбинация волновых функций отдельных независимых структур:
$E=E\left(c_{1} ,c_{2} ,...,c_{n} \right)=\int \psi ^{*} \hat{H}\psi dV $ (3)
Для нахождения коэффициентов $c_{i} $ используется условие минимума:
$\frac{\partial E}{\partial c_{1} } =0,\, \, \, \, \, \, \frac{\partial E}{\partial c_{2} } =0,\, \, \, .....\frac{\partial E}{\partial c_{n} } =0\, $ (4)
Приравнивание первой производной функции нулю есть условие минимума. Решение системы (3) дает значения коэффициентов $c_{1} ,c_{2} ,...c_{n} $.
В качестве примера рассмотрим молекулу $C_{6} H_{6} $. Число независимых структур для молекулы $C_{6} H_{6} $ равно 5.
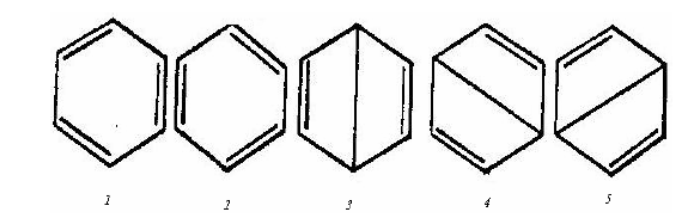
Рисунок 1.
Известно, что в молекуле $C_{6} H_{6} $ длины связей между соседними атомами углерода одинаковы, т.е. они эквивалентны.
Как видно из рисунка, I и II, схемы эквивалентны. Они известны как схемы Кеккуле, а $III - IV - V$ -- как схемы Дьюара для $\pi $-связей $C_{6} H_{6} $. Один из основных принципов $MBC$ заключается в том, что коротким связям соответствует более низкая энергия. С этой точки зрения $I$ и $II$ схемы энергетически более выгодны. Тем не менее предполагается, что молекула пребывает во всех структурах. Волновую функцию молекулы, учитывая эквивалентность схем, $c_{1} =c_{2} ;\, \, c_{3} =c_{4} =c_{5} $ можно написать в следующем виде:
$\begin{array}{l} {\frac{\partial E}{\partial c_{1} } =0,\, \, \, \, \, \, \frac{\partial E}{\partial c_{n} } =0\, } \\ {E(c_{1} ,c_{2} )=\int \psi ^{*} \hat{H}\psi dV} \end{array}$ (5)
Применение $MBC$ к сложным молекулам приводит к большим трудностям при расчетах. Кроме того, существует ряд принципиальных трудностей. Например, этот метод не может объяснить возникновение одноэлектронной химической связи. Кроме того не ясно, какова роль непарных электронов в образовании химической связи.


















