Что изучает молекулярная физика
Молекулярная физика изучает макроскопические процессы в телах с точки зрения атомно-молекулярного строения вещества. Она рассматривает теплоту, как беспорядочное движение микрочастиц. Вообще говоря, этот раздел физики уделяет внимание так же свойствам и строению отдельных молекул и атомов. Молекулярную физику часто называют молекулярно - кинетической теорией вещества (МКТ).
В XIX веке в эпоху зарождения МКТ, во времена, когда само существование молекул и атомов подвергалось сомнению, строгое отделение молекулярной физики от термодинамики было оправдано. Следовало отделить достоверные факты от гипотез неверных. Но когда XX век неопровержимо доказал и нашел методы структурного исследования вещества, МКТ утратила свой гипотетический характер, который имела в начале своего зарождения. Гипотетический элемент молекулярной физики остался только в отношении упрощенных моделей, которыми до сих пор она пользуется при описании и объяснении тех или иных явлений.
Необходимость в таких моделях не утратила своей актуальности, поскольку мы до сих пор не обладаем всей полнотой информации о молекулярной структуре тел. Однако, надо сказать, что теперь четкое отделение МКТ от термодинамики стало не актуальным. В настоящее время при изложении тех или иных положений термодинамики используют выводы, которые получены в МКТ и наоборот. Говорят, что МКТ и термодинамика дополняют друг друга.
Изучать процессы, которые протекают в больших системах весьма сложно из-за огромного числа частиц и их малых размеров. Рассмотреть отдельно каждую частицу практически невозможно, вводятся статистические величины: средняя скорость частиц, их концентрация, масса частицы. Возникает необходимость, установления математической связи (уравнения) между микро параметрами, которые относят к отдельным частицам (масса молекулы, ее скорость и т.д.) и макро параметрами описывающими систему в целом (температура, давление) Формула, характеризующая состояние системы с учетом микроскопических и макроскопических параметров, называется основным уравнением молекулярно-кинетической теории газов).
Статистический метод
Метод, который часто использует молекулярная физика, при рассмотрении предметов или явлений называется статистическим. Статистический метод состоит в изучении свойств макроскопических систем на основе анализа, с помощью методов математической статистики, законов теплового движения большого числа частиц, образующих эти системы.
Самой простой, но информативной моделью, которую мы часто будем использовать в МКТ, будет модель -- идеальный газ. В таком газе молекулы совершают свободное (изолированное от других молекул) движение, лишь время от времени сталкиваясь друг с другом или со стенками сосуда.
Задание: В начальный момент времени t=0 газ температуры T занимает полупространство $x
Решение:
Запишем кинетическое уравнение с учетом того, столкновений молекул нет:
$\frac{\partial f}{\partial t}+\overrightarrow{v}\frac{\partial f}{\partial \overrightarrow{r}}=0$ (1.1)общее решение уравнения (1.1) есть$:\ f=f\left(\overrightarrow{r}-\overrightarrow{v}t,\ \overrightarrow{v}\right).\ $ Используем начальное условие, запишем: $f=f_0\left(v\right)\ при\ v_x>\frac{x}{t},\ f=0\ при\ v_x
где $f_0\left(v\right)$ распределение Максвелла молекул по скоростям ($dN_{v_xv_yv_z}=Nf\left(v\right)dv_x{dv}_y{dv}_z$).
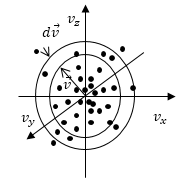
Рис.1
Плотность газа:
\[N\left(t,x\right)=\int\nolimits^{\infty }{\int\nolimits_{-\infty }{\int\nolimits^{\infty }_{\frac{x}{t}}{f_0\left(v\right)m^3dv_xdv_ydv_z}=\frac{N_0}{2}}}\left[1-S(\frac{x}{t}\sqrt{\frac{m}{2T}})\right],\]где $S\left(\varepsilon \right)=\frac{2}{\sqrt{\pi }}\int\nolimits^{\varepsilon }_0{e^{-y^2}dy}$, $N_0\ $- начальная плотность.
Необходимо отметить, что если пренебречь столкновениями молекул, то полученные формулы верны, лишь в области $\left|x\right|\ll l.$
Ответ: Распределение плотности молекул, если молекулы не сталкиваются между собой, определяется формулой: $N\left(t,x\right)=\int\nolimits^{\infty }{\int\nolimits_{-\infty }{\int\nolimits^{\infty }_{\frac{x}{t}}{f_0\left(v\right)m^3dv_xdv_ydv_z}=\frac{N_0}{2}}}\left[1-S(\frac{x}{t}\sqrt{\frac{m}{2T}})\right],$
где $S\left(\varepsilon \right)=\frac{2}{\sqrt{\pi }}\int\nolimits^{\varepsilon }_0{e^{-y^2}dy}$.
Задание: На рис. 1 представлен процесс в идеальном газе при постоянном объеме и переменной массе. Как изменяется масса газа в данном процессе?
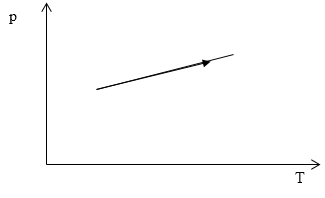
Рис. 2
Решение:
Процесс, заданный на рис. 2 аналитически представим в виде:
\[p=b+aT\left(2.1\right),\]где $b$, $a$ -- постоянные величины, $p$ -- давление, $T$ -- термодинамическая температура.
Процесс в задаче протекает при постоянном объеме, но назвать его изохорным мы не можем, так как масса является переменной. В качестве основания для решения используем уравнение состояния идеального газа (в виде уравнения Менделеева-Клайперона):
\[pV=\frac{m}{\mu }RT\left(2.2\right),\]где V-- объем газа, $m$ -- масса газа, $\mu $-- молярная масса газа, $R$ -- универсальная газовая постоянная.
Выразим из (2.2) массу газа, получим:
\[m=\frac{pV\mu }{RT}\left(2.3\right).\]Учтем, что $V=const$, $\mu =const$ в заданном процессе, тогда запишем:
\[m\sim \frac{p}{T}\left(2.4\right).\]Подставим вместо давления уравнение (2.1), которое задает процесс, получим пропорциональность:
\[m\sim \frac{b+aT}{T}\sim \frac{b}{T}+a\left(2.5\right).\]Исходя из пропорциональности (2.5) видим, что в ходе процесса, который представлен на рис.1, если температура газа увеличивается, масса газа уменьшается.
Ответ: В заданном процессе масса газа уменьшается.












