Классическая двоичная система счисления, как мы знаем, используется для представления информации в компьютере, однако она имеет существенные недостатки, которые влияют на скорость работы процессора.
Один из недостатков – это проблематичное представление отрицательных чисел.
Мы привыкли к традиционному обозначению отрицательных чисел в десятичной системе счисления, помечаем их специальным знаком. Добавление еще одного знака к десяти имеющимся особой роли не играет. Добавление одного знака к имеющимся двум увеличивает число знаков в полтора раза! Поэтому принимались разные попытки записывать отрицательные числа, используя только знаки $0$ и $1$. Прямой код записывается путем добавления в старший бит цифры $0$ для положительных и цифры $1$ для отрицательных чисел. Обратный код записывается путем замены всех цифр регистра, где хранится отрицательное число, на противоположные ($0$ на $1$, $1$ на $0$). В старшем бите при этом отображается знак числа.
В целях повышения быстродействия компьютера, работа которого основывается на использовании двоичной системы, разработчики ввели особое беззнаковое представление отрицательных целых чисел — так называемый дополнительный код. В результате операция вычитания стала выполняться аналогично операции сложения.
То есть, если число записывается с помощью $8$ бит, то имеем:
$01111111=0\cdot (-128)+1\cdot 64+1\cdot 32+...+1\cdot 1=127$, а
$11111111=1\cdot (-128)+1\cdot 64+...+1\cdot 1=-1$.
Однако необходимо отметить, что в данном случае имеется много подводных камней. При сложении чисел нужно проверять, появился ли перенос в самый старший разряд - он тоже должен войти с обратным знаком. Следовательно, самый старший разряд должен обрабатываться совсем не так, как все остальные. Особая предосторожность нужна, если расширили $8$-битное число до $16$ бит. Нельзя просто добавить нули слева. Если число отрицательное, слева необходимо добавить единицы, иначе будет ошибка.
Троичная система счисления – это позиционная система счисления с основанием $3$. Данная система может быть представлена в виде:
-
несимметричной (цифры $0$, $1$, $2$);
-
симметричной (цифры $-1$, $0$, $1$).
Симметричную систему счисления называют также уравновешенной, она была предложена математиком Леонардо Пизано Фибоначчи ($1170 – 1228$) для решения «задачи о гирях».
Требуется подобрать такой набор из $4$ гирь, чтобы с их помощью на чашечных весах можно было взвесить любой груз массой от $1$ до $40$ кг включительно. При необходимости гири можно располагать на обеих чашах весов.
Ответ: искомый набор состоит из гирь в $1$, $3$, $9$ и $27$ кг.
При взвешивании $1$ кг запись может выглядеть следующим образом:
$0 \ 0 \ 0 \ 1_3$.
При взвешивании $2$ кг требуется использовать $2$ гири: на пустую чашу весов поместить гирю в $3$ кг, а на чашу с грузом - в $1$ кг. Результат этого взвешивания записывается в виде: $0 \ 0 \ 1 \ -1_3$.
При взвешивании $4$ кг запись выглядит следующим образом: $0 \ 0 \ 1 \ 1_3$.
Сложнее выражается взвешивание груза в $5$ кг: $0 \ 1 \ -1 \ -1_3$. При этом запись означает, что на пустую чашу помещена гиря, масса которой равна единице $3$ разряда в троичной системе счисления, то есть $9$, а на чашу с грузом помещены гири в $1$ и $3$ кг.
Из приведенных записей видно, что если перед цифрой того или иного разряда стоит минус, то это означает, что гиря соответствующей массы помещена на чашу с грузом и ее масса вычитается из общей массы. Иначе говоря, цифра $" -1"$ - отрицательная единица.
Действительно:
$0 \ 1 \ -1 \ -1_3 = 0\cdot 3^3 + 1\cdot 3^2 - 1\cdot 3^1 - 0\cdot 3^0 = 5_{10}$.
Приведем несколько других записей результатов взвешивания:
-
$0 \ 1 \ -1 \ 0_3 = 0\cdot 3^3 + 1\cdot 3^2 - 1\cdot 3^1 + 0\cdot 3^0 = 6_{10}$;
-
$0 \ 1 \ -1 \ 1_3 = 0\cdot 3^3 + 1\cdot 3^2 - 1\cdot 3^1 + 1\cdot 3^0 = 7_{10}$;
-
$0 \ 1 \ 0 \ - 1_3 = 0\cdot 3^3 + 1\cdot 3^2 + 0\cdot 3^1 - 1\cdot 3^0 = 8_{10}$.
Из записей следует, что результат любого взвешивания на чашечных весах выражается числом, записанным в системе счисления с основанием $P=3$.
Благодаря тому, что основание $3$ нечетно, в троичной системе возможно симметричное относительно нуля расположение цифр: $-1$, $0$, $1$, с которым связано два ценных свойства: естественность представления отрицательных чисел и отсутствие проблемы округления.
Симметричная троичная система наиболее экономна с точки зрения представления чисел.
Если не использовать значение «неизвестно», троичная логика сводится к обычной двоичной логике.
Представления чисел в троичной системе
В таблице приведены примеры представления целых положительных чисел в несимметричной троичной системе счисления:
Рисунок 1.
Если в десятичной системе счисления имеется $10$ цифр и веса соседних разрядов различаются в $10$ раз (разряд единиц, разряд десятков, разряд сотен), то в троичной системе используются только три цифры и веса соседних разрядов различаются в три раза (разряд единиц, разряд троек, разряд девяток, …).
В следующей таблице приведены примеры представления чисел в троичной уравновешенной системе счисления. Глядя на таблицу, понятно, почему эту систему назвали уравновешенной, или симметричной. Очевидно, знак для представления отрицательных чисел не нужен!
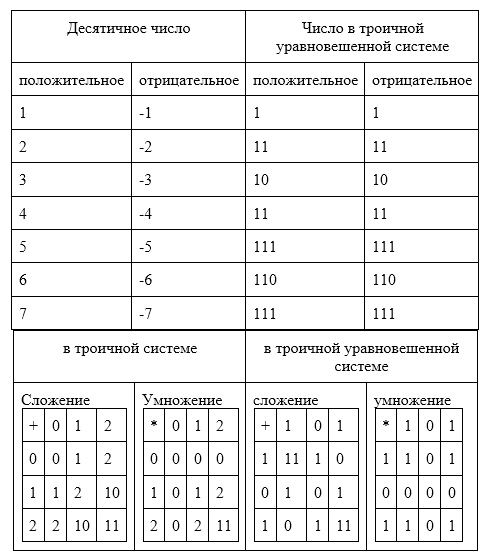
Рисунок 2.
Представление отрицательных чисел
Наличие положительной и отрицательной цифр позволяет непосредственно представлять как положительные, так и отрицательные числа. При этом нет необходимости использовать специальный разряд для знака и не нужно вводить дополнительный (или обратный) код для выполнения арифметических операций с относительными числами. Все действия над числами, представленными в троичной системе счисления с цифрами $0$, $1$, $-1$, выполняются естественно с учетом знаков чисел. Знак числа определяется знаком старшей значащей цифры числа: если она положительна, то и число положительно, если отрицательно, то и число отрицательно. Для изменения знака числа нужно изменить знаки всех его цифр (т.е. инвертировать его код).
Например, записи: $10-1= 8$, $-101= −8$.
Преимущества троичной уравновешенной системы счисления
Благодаря тому, что основание $3$ нечетно, в троичной системе возможно использование расположения цифр, симметричного относительно нуля: $-1$, $0$, $1$. Это дает следующие преимущества: естественность представления отрицательных чисел и отсутствие проблемы округления.
Для изменения знака у представляемого числа на противоположный необходимо изменить знаки у всех цифр, из которых оно состоит. Это свойство увеличивает число операций при перемене знака (в несимметричных системах изменяется только один знаковый разряд), но в то же время повышает надёжность при сбоях в одном или более разрядах.
Процесс округления числа в данной системе счисления заключается в следующем: абсолютная величина части числа, представленной отбрасываемыми младшими цифрами, никогда не превосходит половины абсолютной величины части числа, соответствующей младшей значащей цифре младшего из сохраняемых разрядов. Следовательно, в результате отбрасывания младших цифр числа получаем наиболее выгодное при данном количестве оставшихся цифр приближение, соответственно округление не требуется.
Применение троичной уравновешенной системы счисления в ЭВМ
Главная особенность уравновешенных систем счисления – отсутствие перед отрицательными числами знака "минус" и необходимости анализа знакового операнда при выполнении арифметических операций – стала привлекательной для конструкторов ЭВМ. Так в Советском Союзе в $1958$ году была создана экспериментальная модель ЭВМ, арифметика которой базировалась на использовании троичной уравновешенной системы счисления.
Инициаторами разработки этой уникальной машины стали математики вычислительного центра Московского государственного университета имени М.В. Ломоносова во главе с академиком С.Л. Соболевым и при участии Н.П. Бруснецова и С.П.Маслова. В $1962-1965$ годах было выпущено более $50$ промышленных экземпляров ЭВМ "Сетунь". Особенности этой машины до сих пор привлекают внимание ученых и конструкторов, поскольку в ней, по мнению главного конструктора Н.П. Бруснецова, реализованы далеко не все полезные свойства трехзначного кода и трехзначной логики. Кроме того, в "Сетуни" не были предусмотрены операции над числами с плавающей запятой, для которых преимущества троичного кода особенно существенны. Несмотря на это, машина наглядно продемонстрировала выгодность использования троичного кода. Кроме того, она была гораздо дешевле машин ее класса и превосходила их по быстродействию.











