Непозиционные системы счисления

Единичная система счисления

Необходимость в записи чисел стала возникать у людей еще в древности после того, как они научились считать. Свидетельством этого являются археологические находки в местах стойбищ первобытных людей, которые относятся к периоду палеолита ($10$-$11$ тыс. лет до н.э.). Изначально количество предметов изображали, используя определенные знаки: черточки, насечки, кружочки, нанесенные на камни, дерево или глину, а также узлы на веревках.

Рисунок 1.

Ученые эту систему записи чисел называют единичной (унарной), поскольку число в ней образовано повторением одного знака, который символизирует единицу.

Недостатки системы:

• при написании большого числа необходимо использовать большое количество палочек;

• возможно легко ошибиться при нанесении палочек.

Позднее, чтобы облегчить счет, эти знаки люди стали объединять.

Единичная система не совсем удобна, так как записи выглядят очень длинно и их нанесение довольно утомительно, поэтому со временем стали появляться более практичые в использовании системы счисления.

Вот некоторые примеры.

Древнеегипетская десятичная непозиционная система счисления

Данная система счисления появилась около 3000 лет до н.э. в результате того, что жители Древнего Египта придумали свою числовую систему, в которой при обозначении ключевых чисел $1$, $10$, $100$ и т.д. были использованы иероглифы, что было удобным при написании на глиняных дощечках, которые заменяли бумагу. Другие числа составлялись из них с помощью сложения. Сначала записывалось число высшего порядка, а затем низшего. Умножали и делили египтяне, последовательно удваивая числа. Каждая цифра могла повторяться до $9$ раз. Примеры чисел данной системы приведены ниже.

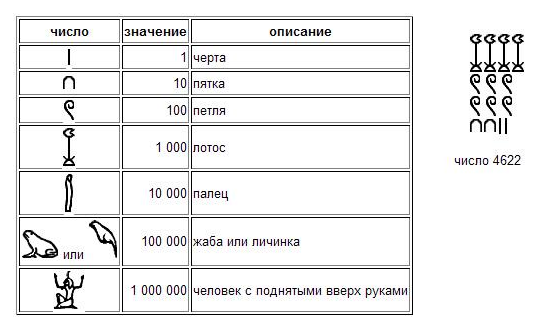
Рисунок 2.

Римская система счисления

Данная система принципиально не намного отличается от предыдущей и сохранилась до наших дней. В ее основе находятся знаки:

• $I$ (один палец) для числа $1$;

• $V$ (раскрытая ладонь) для числа $5$;

• $X$ (две сложенные ладони) для $10$;

• для обозначения чисел $100$, $500$ и $1000$ использовались первые буквы соответствующих латинских слов (Сentum – сто, Demimille – половина тысячи, Мille – тысяча).

При составлении чисел римляне использовали следующие правила:

1. Число равно сумме значений расположенных подряд нескольких одинаковых «цифр», образующих группу первого вида.

2. Число равно разности значений двух «цифр», если слева от большей стоит меньшая. В этом случае от значения большей отнимается значение меньшей. Вместе они образуют группу второго вида. При этом левая «цифра» может быть меньше правой максимально на $1$ порядок: перед $L(50)$ и $C(100$) из «младших» может стоять только $Х(10$), перед $D(500$) и $M(1000$) – только $C(100$), перед $V(5) – I(1)$.

3. Число равно сумме значений групп и «цифр», не вошедших в группы $1$ или $2$ вида.

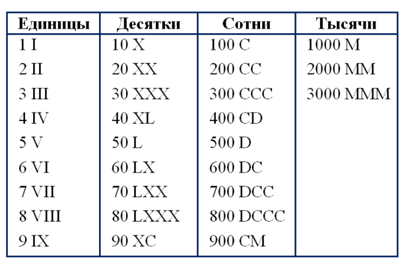
Рисунок 3.

Римскими цифрами пользуются издревле: ими обозначаются даты, номера томов, разделов, глав. Раньше считал, что обычные арабские цифры можно легко подделать.

Алфавитные системы счисления

Данные системы счисления более совершенны. К ним относятся греческая, славянская, финикийская, еврейская и другие. В этих системах числа от $1$ до $9$, а также количество десятков (от $10$ до $90$), сотен (от $100$ до $900$) были обозначены буквами алфавита.

В древнегреческой алфавитной системе счисления числа $1, 2, ..., 9$ обозначались первыми девятью буквами греческого алфавита, и т.д. Для обозначения чисел $10, 20, ..., 90$ применялись следующие $9$ букв а для обозначения чисел $100, 200, ..., 900$ – последние $9$ букв.

У славянских народов числовые значения букв устанавливались в соответствии с порядком славянского алфавита, использовавшего изначально глаголицу, а затем кириллицу.

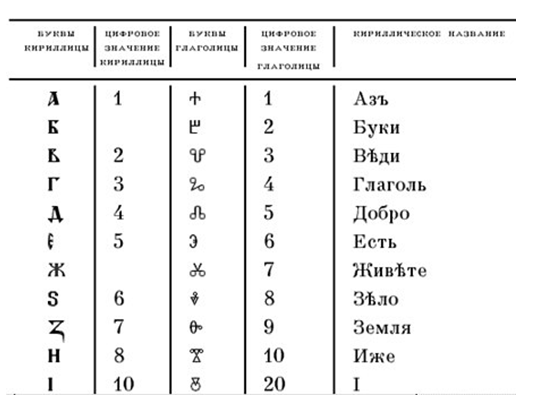
Рисунок 4.

Непозиционные системы счисления имеют ряд существенных недостатков:

• Существует постоянная потребность введения новых знаков для записи больших чисел.

• Невозможно представлять дробные и отрицательные числа.

• Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения.