В $60$-х и $70$-х гг. не было единопризнанного стандарта представления чисел с плавающей запятой, из-за чего программы того времени не были переносимыми приложениями. Также большой проблемой были «странности» разных компьютеров, которые нужно было знать и учитывать при создании программ.
В $1976$ году была появилась инициатива создать единый стандарт для представления чисел с плавающей запятой, что существенно упростило работу с числами.
Вычисления компьютера ограничены его памятью, поэтому дробная часть вещественных чисел не является бесконечной и хранится в памяти с определенной точностью.
Числа в нормализованном виде чаще всего записываются только на экране компьютера, поэтому принято запятую в них заменять на точку.
Принятый способ хранения вещественных (действительных) чисел в памяти компьютера использует нормализованную (экспоненциальную) запись действительных чисел.
Для хранения вещественных чисел (как и для целых) используется двоичная система. Таким образом, число предварительно должно быть переведено двоичный код.
Нормализованная запись числа
Запись в виде
\[a=\pm m\cdot q^n\]является нормализованной записью отличного от нуля действительного числа,
где $n$ -- любое целое число (в том числе и ноль),
$m$ -- правильная дробь в системе счисления с основой $q$, у которой первая цифра после запятой не равна нулю, то есть $\frac{1}{q}\le m
$m$ называется мантиссой числа, $n$ -- порядком числа, $q$ -- основанием системы счисления.
Приведем числа десятеричной системы к нормализованной записи:
\[1.3579=0.13579\cdot {10}^1;\] \[10000=0.1\cdot {10}^5;\] \[0,123456=0.123456\cdot {10}^0.\]Приведем число восьмеричной системы счисления к нормализованной записи:
${0,0000119}_8={0.119}_8\cdot 8^{-4}$ (порядок записан в десятичной системе).
Приведем число двоичной системы счисления к нормализованной записи:
\[{200.002}_2={0.200002}_2\cdot 2^{-3}.\]Ноль в десятичной системе будет записан в нормализованном виде следующим образом:
Нормализованная экспоненциальная запись (НЭЗ) числа - это запись в виде
\[a=\pm m\cdot q^n,\]где $n$ -- любое целое число (в том числе и ноль),
$m$ -- правильная дробь в системе счисления с основой $q$, целая часть которой состоит из одной цифры,
$m$ --мантисса числа, а $n$ -- порядок (или экспонента) числа.
Рассмотрим вышеописанные числа в нормализованной экспоненциальной записи.
НЭЗ десятичных чисел:
\[1.3579=0.13579\cdot {10}^1=1.3579\cdot {10}^0;\] \[10000=0.1\cdot {10}^5=1.0\cdot {10}^4;\] \[0.123456=0.123456\cdot {10}^0=1.23456\cdot {10}^{-1}.\]НЭЗ восьмеричного числа:
\[{0.0000119}_8={0.119}_8\cdot 8^{-4}={1.19}_8\cdot 8^{-5}.\]НЭЗ двоичного числа:
\[{200.002}_2={0.200002}_2\cdot 2^{-3}={2.00002}_2\cdot 2^{-4}.\]Обратите внимание, что в НЭЗ записи первая цифра после запятой может быть нулём, в отличие от нормализованной записи.
Хранение чисел с плавающей запятой
Для хранения вещественных чисел в памяти компьютера часть разрядов ячейки отводится для записи порядка числа, остальные -- для записи мантиссы. По одному разряду в каждой группе разрядов отводится для знака порядка и знака мантиссы. Чтобы не хранить знак порядка был придуман смещенный порядок.
Если для задания порядка выделено k разрядов, то к истинному порядку (ИП) прибавляют смещение, таким образом, смещённый порядок (СП) рассчитывается по формуле:
Найдем смещённый порядок для истинного порядка, лежащего в диапазоне от $-127$ до $+128$.
Возьмем начальное значение ИП= $-127$:
\[СП=-127+2^{8-1}-1=-127+128-1=0.\]Возьмем конечное значение ИП = $128$:
\[СП=128+2^{8-1}-1=128+128-1=255.\]Таким образом, ИП, лежащий в диапазоне от $-127$ до $+128$, представляется смещённым порядком, значения которого меняются в диапазоне от $0$ до $255$.
Алгоритм представления вещественного числа:
-
Перевести число в двоичную систему счисления.
-
Привести число к нормализованной записи.
-
Найти смещённый порядок числа.
-
Поместить знак, порядок и мантиссу в соответствующие разряды.
Представим число $-25.625$ в $4$-байтовом представлении ($1$ бит отводится под знак числа, $8$ бит -- под смещённый порядок, остальные биты -- под мантиссу).
Будем действовать по алгоритму:
-
Переведем число $-25.625$ в двоичный код:
\[{25}_{10}={11001}_2\]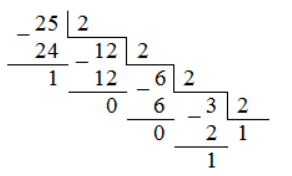
Рисунок 1.
\[{25}_{10}={11001}_2\] \[{0.625}_{10}={0.101}_2\] \[{-25.625}_{10}={-11001.101}_2\]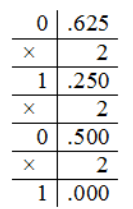
Рисунок 2. -
Приведем число к нормализованному виду:
\[{-11001.101}_2={-1.1001101}_2\cdot 2^4\] -
Найдем смещенный порядок числа:
\[СП=127+4=131\] -
Поместим знак, порядок и мантиссу в соответствующие разряды:

Рисунок 3.











