История развития компьютерной арифметики
Целью разработки компьютеров было автоматизировать выполнение расчетов, облегчить процесс вычислений. Первые вычислительные машины, которые выполняли четыре арифметические операции (сложение, вычитание, умножение и деление), были сконструированы в XVII столетии.
Счетная машина Шиккарда
В $1623$ г. Вильгельм Шиккард, немецкий ученый, математик, астроном, сконструировал машину, автоматически выполняющую операции сложения, вычитания, умножения и деления. Счетная машина содержала суммирующее, множительное устройства и механизм для записи промежуточных результатов. Разработка машины Шиккарда не стала достаточно известной, поэтому принципы ее работы не существенно повлияли на дальнейшее развитие вычислительной техники, но признана первооткрывательницей эры механической вычислительной техники.

Рисунок 1. Арифметическая машина Шиккарда
Суммирующая машина Паскаля
Машина Паскаля (названная «Паскалина») была разработана французским ученым в $1641$ г. ($1643$ г. по другим данным) для выполнения финансовый расчётов, которыми занимался его отец. Принцип действия Паскалины был как у машины Шиккарда с одним отличием – в машине Паскаля был реализован автоматический перенос единицы в следующий разряд при полном обороте колеса предыдущего разряда (так же, как при сложении десятичных чисел в следующий разряд числа переносятся десятки, которые образовались в результате сложения единиц, сотни – в результате сложения десятков). Такое решение давало возможность выполнять сложение многозначных чисел автоматически, без человеческого вмешательства в работу механизма. Этот принцип использовался с середины XVII до XX века при построении механических арифмометров и электрических вычислительных машин.

Рисунок 2. Паскалина
Арифмометр Лейбница
Арифмометр был создан немецким математиком Готфридом В. Лейбницем в $1673$ г. Выполнение операции сложения чисел выполнялось как на Паскалине – при помощи связанных между собой колёс. В конструкцию была добавлена движущаяся часть и специальная рукоятка, которая позволяла крутить ступенчатое колесо (в последующем заменено на цилиндры), что ускоряло повторяющиеся операции сложения, при помощи которых выполнялось умножение и деление чисел. Необходимое количество повторных сложений выполнялось автоматически. Машина Лейбница могла выполнять четыре арифметические операции в десятичной системе счисления.

Рисунок 3. Копия арифмометра Лейбница в Немецком музее
Арифмометр Однера
Арифмометр разработан в $1873$ г. русским механиком В.Т. Однером.

Рисунок 4. Арифмометр Однера
Арифмометр являлся успешным образцом, но все же массовое изготовление таких машин всё ещё было невыгодным. Попытки усовершенствовать арифмометр тянулись весь XVIII век и только в XIX веке арифмометры стали широко распространены.

Рисунок 5. Арифмометр 1932 г. выпуска
В XX веке на смену механическим вычислительным машинам пришли электронные, в основе которых лежат алгоритмы, использующие минимальное число элементарных операций для выполнения арифметических операций.
Особенности представления чисел в компьютере
Представлением числа в компьютере называют его представление в разрядной сетке машины. В вычислительных машинах применяются две формы представления чисел:
- естественная форма (с фиксированной запятой);
- нормальная форма (с плавающей запятой).
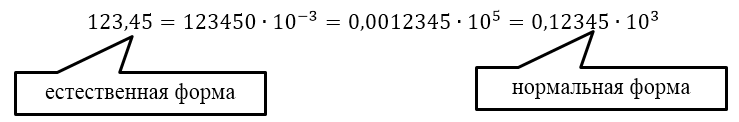
Рисунок 6.
Всякое десятичное число, прежде чем оно попадает в память компьютера, преобразуется из десятичной системы счисления в двоичную. Форма с фиксированной запятой применяется к целым числам (как положительным, так и отрицательным), форма с плавающей запятой – к вещественным числам (целым и дробным). Под запятой подразумевается знак-разделитель целой и дробной части числа.
Диапазон чисел, представляемых в компьютере, измеряется значением $2^n$, где $n$ – разрядность двоичного числа.
Если числа только положительные, то они называются беззнаковыми целыми.
Для представления положительных и отрицательных чисел используются такие формы представления, как:
- код со смещением;
- прямой код;
- дополнительный код – наиболее удобная форма для представления отрицательных чисел при выполнении арифметических операций посредством компьютера. Форма дополнительного кода сложна для понимания, но очень хорошо подходит для выполнения арифметических действий.
Формы представления чисел в формате с плавающей запятой сложнее, чем в формате с фиксированной запятой. Основная идея – мантисса умножается на число $10$ в степени, равной экспоненте.

Рисунок 7.
Такая форма записи является удобной для представления очень больших и очень маленьких чисел.
В памяти компьютера форма представления числа с плавающей запятой использует основание, равное $2$, а не $10$:
$1,2345 \cdot 2^{10}$.
Числа с плавающей запятой являются нормализованными, т.е. только одна цифра, не равная нулю, располагается слева от десятичной точки (называется двоичной точкой). Для числа по основанию $2$ существует только одна цифра, не равная нулю – это $1$. Поэтому для мантиссы эта цифра всегда равна $1$ и ее можно не записывать.












