Растры, пиксели, дискретизация, разрешение
Как и все виды информации, изображения в компьютере закодированы в виде двоичных последовательностей. Используют два принципиально разных метода кодирования, каждый из которых имеет свои достоинства и недостатки.
И линия, и область состоят из бесконечного числа точек. Цвет каждой из этих точек нам нужно закодировать. Если их бесконечно много, мы сразу приходим к выводу, что для этого нужно бесконечно много памяти. Поэтому «поточечным» способом изображение закодировать не удастся. Однако, эту все-таки идею можно использовать.
Начнем с черно-белого рисунка. Представим себе, что на изображение ромба наложена сетка, которая разбивает его на квадратики. Такая сетка называется растром. Теперь для каждого квадратика определим цвет (черный или белый). Для тех квадратиков, в которых часть оказалась закрашена черным цветом, а часть белым, выберем цвет в зависимости от того, какая часть (черная или белая) больше.
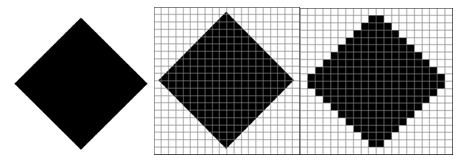
Рисунок 1.
У нас получился так называемый растровый рисунок, состоящий из квадратиков-пикселей.
Пиксель (англ. pixel = picture element, элемент рисунка) – это наименьший элемент рисунка, для которого можно задать свой цвет. Разбив «обычный» рисунок на квадратики, мы выполнили его дискретизацию – разбили единый объект на отдельные элементы. Действительно, у нас был единый и неделимый рисунок – изображение ромба. В результаты мы получили дискретный объект – набор пикселей.
Двоичный код для черно-белого рисунка, полученного в результате дискретизации можно построить следующим образом:
- заменяем белые пиксели нулями, а черные – единицами;
- выписываем строки полученной таблицы одну за другой.
Покажем это на простом примере:

Рисунок 2.
Ширина этого рисунка – $8$ пикселей, поэтому каждая строчка таблицы состоит из $8$ двоичных разрядов – битов. Чтобы не писать очень длинную цепочку нулей и единиц, удобно использовать шестнадцатеричную систему счисления, закодировав $4$ соседних бита (тетраду) одной шестнадцатеричной цифрой.

Рисунок 3.
Например, для первой строки получаем код $1A_{16}$:
а для всего рисунка: $1A2642FF425A5A7E_{16}$.
Очень важно понять, что мы приобрели и что потеряли в результате дискретизации. Самое важное – мы смогли закодировать рисунок в двоичном коде. Однако при этом рисунок исказился - вместо ромба мы получили набор квадратиков. Причина искажения в том, что в некоторых квадратиках части исходного рисунка были закрашены разными цветами, а в закодированном изображении каждый пиксель обязательно имеет один цвет. Таким образом, часть исходной информации при кодировании была потеряна. Это проявится, например, при увеличении рисунка - квадратики увеличиваются, и рисунок еще больше искажается. Чтобы уменьшить потери информации, нужно уменьшать размер пикселя, то есть увеличивать разрешение.
Разрешение – это количество пикселей, приходящихся на дюйм размера изображения.
Разрешение обычно измеряется в пикселях на дюйм (используется английское обозначение $ppi$ = pixels per inch). Например, разрешение $254$ $ppi$ означает, что на дюйм ($25,4$ мм) приходится $254$ пикселя, так что каждый пиксель «содержит» квадрат исходного изображения размером $0,1×0,1$ мм. Чем больше разрешение, тем точнее кодируется рисунок (меньше информации теряется), однако одновременно растет и объем файла.
Кодирование цвета
Что делать, если рисунок цветной? В этом случае для кодирования цвета пикселя уже не обойтись одним битом. Например, в показанном на рисунке изображении российского флага $4$ цвета: черный, синий, красный и белый. Для кодирования одного из четырех вариантов нужно $2$ бита, поэтому код каждого цвета (и код каждого пикселя) будет состоять из двух бит. Пусть $00$ обозначает черный цвет, $01$ – красный, $10$ – синий и $11$ – белый. Тогда получаем такую таблицу:
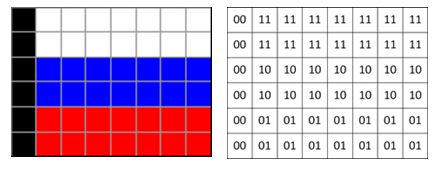
Рисунок 4.
Проблема только в том, что при выводе на экран нужно как-то определить, какой цвет соответствует тому или другому коду. То есть информацию о цвете нужно выразить в виде числа (или набора чисел).
Человек воспринимает свет как множество электромагнитных волн. Определенная длина волны соответствуют некоторому цвету. Например, волны длиной $500-565$ нм – это зеленый цвет. Так называемый «белый» свет на самом деле представляет собой смесь волн, длины которых охватывают весь видимый диапазон.
Согласно современному представлению о цветном зрении (теории Юнга-Гельмгольца), глаз человека содержит чувствительные элементы трех типов. Каждый из них воспринимает весь поток света, но первые наиболее чувствительны в области красного цвета, вторые – области зеленого, а третьи – в области синего цвета. Цвет – это результат возбуждения всех трех типов рецепторов. Поэтому считается, что любой цвет (то есть ощущения человека, воспринимающего волны определенной длины) можно имитировать, используя только три световых луча (красный, зеленый и синий) разной яркости. Следовательно, любой цвет приближенно раскладывается на три составляющих – красную, зеленую и синюю. Меняя силу этих составляющих, можно составить любые цвета. Эта модель цвета получила название RGB по начальным буквам английских слов red (красный), green (зеленый) и blue (синий).
В модели RBG яркость каждой составляющей (или, как говорят, каждого канала) чаще всего кодируется целым числом от $0$ до $255$. При этом код цвета – это тройка чисел (R,G,B), яркости отдельных каналов. Цвет ($0,0,0$) – это черный цвет, а ($255,255,255$) – белый. Если все составляющие имеют равную яркость, получаются оттенки серого цвета, от черного до белого.

Рисунок 5.
Чтобы сделать светло-красный (розовый) цвет, нужно в красном цвете ($255,0,0$) одинаково увеличить яркость зеленого и синего каналов, например, цвет ($255, 150, 150$) – это розовый. Равномерное уменьшение яркости всех каналов делает темный цвет, например, цвет с кодом ($100,0,0$) – тёмно-красный.
Всего есть по $256$ вариантов яркости каждого из трех цветов. Это позволяет закодировать $256^3= 16 777 216$ оттенков, что более чем достаточно для человека. Так как $256 = 2^8$, каждая из трех составляющих занимает в памяти $8$ бит или $1$ байт, а вся информация о каком-то цвете – $24$ бита (или $3$ байта). Эта величина называется глубиной цвета.
Глубина цвета – это количество бит, используемое для кодирования цвета пикселя.
$24$-битное кодирование цвета часто называют режимом истинного цвета (англ. True Color – истинный цвет). Для вычисления объема рисунка в байтах при таком кодировании нужно определить общее количество пикселей (перемножить ширину и высоту) и умножить результат на $3$, так как цвет каждого пикселя кодируется тремя байтами. Например, рисунок размером $20×30$ пикселей, закодированный в режиме истинного цвета, будет занимать $20×30×3 = 1800$ байт.
Кроме режима истинного цвета используется также $16$-битное кодирование (англ. High Color – «высокий» цвет), когда на красную и синюю составляющую отводится по $5$ бит, а на зеленую, к которой человеческий глаз более чувствителен – $6$ бит. В режиме High Color можно закодировать $2^{16} = 65 536$ различных цветов. В мобильных телефонах $12$-битное кодирование цвета ($4$ бита на канал, $4096$ цветов).
Кодирование с палитрой
Как правило, чем меньше цветов используется, тем больше будет искажаться цветное изображение. Таким образом, при кодировании цвета тоже есть неизбежная потеря информации, которая «добавляется» к потерям, вызванным дискретизацией. Очень часто (например, в схемах, диаграммах и чертежах) количество цветов в изображении невелико (не более $256$). В этом случае применяют кодирование с палитрой.
Цветовая палитра – это таблица, в которой каждому цвету, заданному в виде составляющих в модели RGB, сопоставляется числовой код.
Кодирование с палитрой выполняется следующим образом:
- выбираем количество цветов $N$ (как правило, не более $256$);
- из палитры истинного цвета ($16 777 216$ цветов) выбираем любые $N$ цветов и для каждого из них находим составляющие в модели RGB;
- каждому из цветов присваиваем номер (код) от $0$ до $N–1$;
- составляем палитру, записывая сначала RGB-составляющие цвета, имеющего код $0$, затем составляющие цвета с кодом $1$ и т.д.
Цвет каждого пикселя кодируется не в виде значений RGB-составляющих, а как номер цвета в палитре. Например, при кодировании изображения российского флага (см. выше) были выбраны $4$ цвета:
- черный: RGB-код ($0,0,0$); двоичный код $002$;
- красный: RGB-код ($255,0,0$); двоичный код $012$;
- синий: RGB-код ($0,0,255$); двоичный код $102$;
- белый: RGB-код ($255,255,255$); двоичный код $112$.
Поэтому палитра, которая обычно записывается в специальную служебную область в начале файла (ее называют заголовком файла), представляет собой четыре трехбайтных блока:

Рисунок 6.
Код каждого пикселя занимает всего два бита.
Палитры с количеством цветом более $256$ на практике не используются.
Достоинства и недостатки растрового кодирования
Растровое кодирование имеет достоинства:
- универсальный метод (можно закодировать любое изображение);
- единственный метод для кодирования и обработки размытых изображений, не имеющих четких границ, например, фотографий.
И недостатки:
- при дискретизации всегда есть потеря информации;
- при изменении размеров изображения искажается цвет и форма объектов на рисунке, поскольку при увеличении размеров надо как-то восстановить недостающие пиксели, а при уменьшении – заменить несколько пикселей одним;
- размер файла не зависит от сложности изображения, а определяется только разрешением и глубиной цвета.
Как правило, растровые рисунки имеют большой объем.











