Основные законы алгебры логики

Общие сведения

Для преобразования функций, упрощения формул, полученных при формализации условий логических задач, в алгебре логики производятся эквивалентные преобразования, опирающиеся на основные логические законы. Некоторые из этих законов формулируются и записываются так же, как аналогичные законы в арифметике и алгебре, другие выглядят непривычно.

Законы алгебры логики называют иногда теоремами.

В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул.

В справедливости всех законов можно убедиться, построив таблицы истинности для левой и правой частей записанного закона. После упрощения выражения с применением законов алгебры логики таблицы истинности совпадают.

Справедливость части законов можно доказать, применяя инструментарий таблиц истинности.

Рисунок 1.

Примеры

• Составим таблицу истинности для выражения

  
  
  Рисунок 2.

  В первые два столбца таблицы запишем четыре возможных пары значений $x$ и $y$, в последующих столбцах — значения промежуточных выражений, а в последнем столбце — значение исходного выражения. В результате получим таблицу:

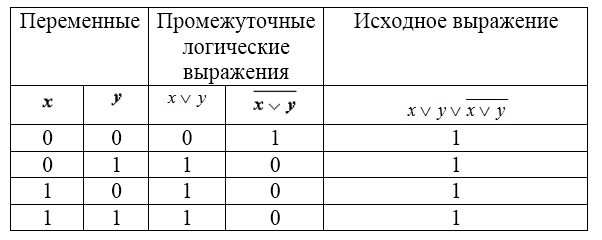
Рисунок 3.

Упростим исходное выражение, используя основные законы алгебры логики:

Рисунок 4.

(закон Де Моргана, распределительный закон для И, закон идемпотенции, операция переменной с её инверсией).

Из таблицы видно, что при всех наборах значений переменных $x$ и $y$ формула на рис.2 принимает значение $1$, то есть является тождественно истинной.

• Составим таблицу истинности для выражения:

  
  
  Рисунок 5.

  , которое содержит две переменные $x$ и $y$. В первые два столбца таблицы запишем четыре возможных пары значений $x$ и $y$, в последующих столбцах — значения промежуточных выражений, а в последнем столбце — значение исходного выражения. В результате получим таблицу:

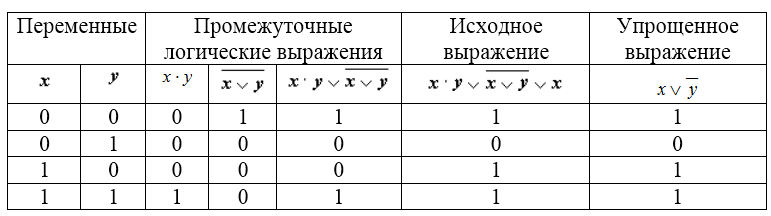
Рисунок 6.

Из таблицы видно, что Исходное выражение принимает такие же значения, что и Упрощенное выражение на соответствующих значениях переменных $x$ и $y$.

Упростим выражение на рис.5, применяя основные законы алгебры логики.

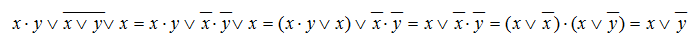
Рисунок 7.

(закон Де Моргана, закон поглощения, распределительный закон для И).

• Составим таблицу истинности для выражения

  
  
  Рисунок 8.

Рисунок 9.

Из таблицы видно, что при всех наборах значений переменных $x$ и $y$ формула на рис.8 принимает значение $0$, то есть является тождественно ложной.

Упростим выражение, применяя законы алгебры логики:

Рисунок 10.

• Упростим выражение:

  
  
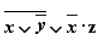
  Рисунок 11.

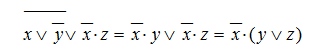
Рисунок 12.

(закон Де Могргана, распределительный).

Составим таблицу истинности для выражения на рис.11:

Рисунок 13.

Из таблицы видно, что выражение на рис.11 в некоторых случаях принимает значение $1$, а в некоторых — $0$, то есть является выполнимым.

• Упростить выражение используя законы алгебры логики:

  
  
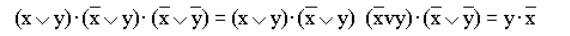
  Рисунок 14.

(правило де Моргана, выносим за скобки общий множитель, правило операций переменной с её инверсией).

• Упростить выражение используя законы алгебры логики:

  
  
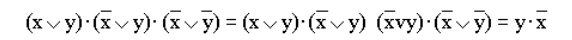
  Рисунок 15.

(повторяется второй сомножитель, что возможно используя закон идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания).

• Упростить выражение используя законы алгебры логики:

  
  
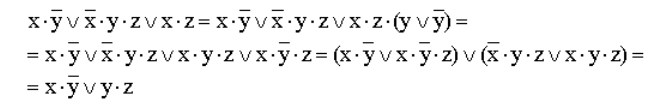
  Рисунок 16.

(вводим вспомогательный логический сомножитель

Рисунок 17.