В соответствии с корпускулярно -- волновым дуализмом в квантовой физике состояние частицы описывается при помощи волновой функции ($\psi (\overrightarrow{r},t)$- пси-функция).
Волновая функция -- это функция, которая используется в квантовой механике. Она описывает состояние системы, которая имеет размеры в пространстве. Она является вектором состояния.
Данная функция является комплексной и формально имеет волновые свойства. Движение любой частицы микромира определено вероятностными законами. Распределение вероятности выявляется при проведении большого числа наблюдений (измерений) или большого количества частиц. Полученное распределение аналогично распределению интенсивности волны. То есть в местах с максимальной интенсивностью отмечено максимальное количество частиц.
Набор аргументов волновой функции определяет ее представление. Так, возможно координатное представление: $\psi(\overrightarrow{r},t)$, импульсное представление: $\psi'(\overrightarrow{p},t)$ и т.д.
В квантовой физике целью ставится не точность предсказания события, а оценка вероятности того или иного события. Зная величину вероятности, находят средние значения физических величин. Волновая функция позволяет находить подобные вероятности.
Так вероятность присутствия микрочастицы в объеме dV в момент времени t может быть определена как:
где $\psi^*$- комплексно сопряженная функция к функции $\psi.$ Плотность вероятности (вероятность в единице объёма) равна:
Вероятность является величиной, которую можно наблюдать в эксперименте. В это же время волновая функция не доступна для наблюдения, так как она является комплексной (в классической физике параметры, которые характеризуют состояние частицы, доступны для наблюдения).
Условие нормировки $\psi$- функции
Волновая функция определена с точностью до произвольного постоянного множителя. Данный факт не оказывает влияния на состояние частицы, которую $\psi$- функция описывает. Однако волновую функцию выбирают таким образом, что она удовлетворяет условию нормировки:
где интеграл берут по всему пространству или по области, в которой волновая функция не равна нулю. Условие нормировки (2) значит то, что во всей области, где $\psi\ne 0$ частица достоверно присутствует. Волновую функцию, которая подчинятся условию нормировки, называют нормированной. Если ${\left|\psi\right|}^2=0$, то данное условие означает, что частицы в исследуемой области наверняка нет.
Нормировка вида (2) возможна при дискретном спектре собственных значений.
Условие нормировки может оказаться не осуществимым. Так, если $\psi$ -- функция является плоской волной де-Бройля и вероятность нахождения частицы является одинаковой для всех точек пространства. Данные случаи рассматривают как идеальную модель, в которой частица присутствует в большой, но имеющей ограничения области пространства.
Принцип суперпозиции волновой функции
Данный принцип является одним их основных постулатов квантовой теории. Его смысл в следующем: если для некоторой системы возможны состояния, описываемые волновыми функциями $\psi_1\ {\rm и}\ $ $\psi_2$, то для этой системы существует состояние:
где $C_{1\ }и\ C_2$ -- постоянные коэффициенты. Принцип суперпозиции подтверждается эмпирически.
Можно говорить о сложении любого количества квантовых состояний:
где ${\left|C_n\right|}^2$ -- вероятность того, что система обнаруживается в состоянии, которое описывается волновой функцией $\psi_n.$ Для волновых функций, подчиненных условию нормировки (2) выполняется условие:
Стационарные состояния
В квантовой теории особую роль имеют стационарные состояния (состояния в которых все наблюдаемые физические параметры не изменяются во времени). (Сама волновая функция принципиально не наблюдаема). В стационарном состоянии $\psi$- функция имеет вид:
где $\omega =\frac{E}{\hbar }$, $\psi\left(\overrightarrow{r}\right)$ не зависит от времени, $E$- энергия частицы. При виде (3) волновой функции плотность вероятности ($P$) является постоянной времени:
Из физических свойств стационарных состояний следуют математические требования к волновой функции $\psi\left(\overrightarrow{r}\right)\to \ (\psi(x,y,z))$.
Математические требования к волновой функции для стационарных состояний
$\psi\left(\overrightarrow{r}\right)$- функция должна быть во всех точках:
- непрерывна,
- однозначна,
- конечна.
Если потенциальная энергия имеет поверхность разрыва, то на подобных поверхностях функция $\psi\left(\overrightarrow{r}\right)$ и ее первая производная должны оставаться непрерывными. В области пространства, где потенциальная энергия становится бесконечной, $\psi\left(\overrightarrow{r}\right)$ должна быть равна нулю. Непрерывность функции $\psi\left(\overrightarrow{r}\right)$ требует, чтобы на любой границе этой области $\psi\left(\overrightarrow{r}\right)=0$. Условие непрерывности накладывается на частные производные от волновой функции ($\frac{\partial \psi}{\partial x},\ \frac{\partial \psi}{\partial y},\frac{\partial \psi}{\partial z}$).
Задание: Для некоторой частицы задана волновая функция вида: $\psi=\frac{A}{r}e^{-{r}/{a}}$, где $r$ -- расстояние от частицы до центра силы (рис.1), $a=const$. Примените условие нормировки, найдите нормировочный коэффициент A.
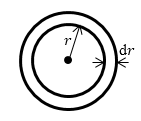
Рисунок 1.
Решение:
Запишем условие нормировки для нашего случая в виде:
\[\int{{\left|\psi\right|}^2dV=\int{\psi\psi^*dV=1\left(1.1\right),}}\]где $dV=4\pi r^2dr$ (см.рис.1 Из условий понятно, что задача обладает сферической симметрией). Из условий задачи имеем:
\[\psi=\frac{A}{r}e^{-{r}/{a}}\to \psi^*=\frac{A}{r}e^{-{r}/{a}}\left(1.2\right).\]Подставим $dV$ и волновые функции (1.2) в условие нормировки:
\[\int\limits^{\infty }_0{\frac{A^2}{r^2}e^{-{2r}/{a}}4\pi r^2dr=1\left(1.3\right).}\]Проведем интегрирование в левой части:
\[\int\limits^{\infty }_0{\frac{A^2}{r^2}e^{-{2r}/{a}}4\pi r^2dr=2\pi A^2a=1\left(1.4\right).}\]Из формулы (1.4) выразим искомый коэффициент:
\[A=\sqrt{\frac{1}{2\pi a}}.\]Ответ: $A=\sqrt{\frac{1}{2\pi a}}.$
Задание: Каково наиболее вероятное расстояние ($r_B$) электрона от ядра, если волновая функция, которая описывает основное состояние электрона в атоме водорода может быть определена как: $\psi=Ae^{-{r}/{a}}$, где $r$- расстояние от электрона до ядра, $a$ -- первый Боровский радиус?
Решение:
Используем формулу, которая определяет вероятность присутствия микрочастицы в объеме $dV$ в момент времени $t$:
\[dP={\left|\psi\right|}^2dV=\psi\psi^*dV\left(2.1\right),\]где $dV=4\pi r^2dr.\ $Следователно, имеем:
\[dP=4\pi r^2A^2e^{-{2r}/{a}}dr\left(2.2\right).\]В таком случае, $p=\frac{dP}{dr}$ запишем как:
\[p=4\pi r^2A^2e^{-{2r}/{a}}\left(2.3\right).\]Для определения наиболее вероятного расстояния производную $\frac{dp}{dr}$ приравняетм к нулю:
\[{\left.\frac{dp}{dr}\right|}_{r=r_B}=8\pi rA^2e^{-{2r}/{a}}+4\pi r^2A^2e^{-{2r}/{a}}\left(-\frac{2}{a}\right)=8\pi rA^2e^{-{2r}/{a}}\left(1-\frac{r}{a}\right)=0(2.4)\]Так как решение $8\pi rA^2e^{-{2r_B}/{a}}=0\ \ {\rm при}\ \ r_B\to \infty $, нам не подходит, то отсается:
\[1-\frac{r_B}{a}=0\to r_B=a.\]Ответ: $r_B=a.$













