Векторы напряженности электрического ($\overrightarrow{E}$) и магнитного ($\overrightarrow{H}$) полей в электромагнитной волне всегда взаимно перпендикулярны, они находятся в плоскости перпендикулярной вектору скорости волны ($\overrightarrow{v}$). Из вышесказанного следует, что электромагнитные волны являются поперечными. Ориентация векторов (взаимная) $\overrightarrow{E}$, $\overrightarrow{H},\ \overrightarrow{v}$ подчиняется правилу: Если смотреть из конца вектора скорости, то вращение от вектора напряжённости электрического поля по кратчайшему направлению к вектору напряженности магнитного поля идет против часовой стрелки (рис.1). Или, вектор $\overrightarrow{v}$ имеет направление, как и векторное произведение $\overrightarrow{E}$ на $\overrightarrow{H}$:
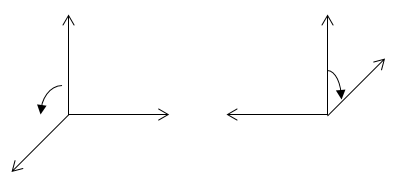
Рисунок 1.
Электромагнитное поле в однородной, изотропной, непроводящей среде, не имеющей сегнетоэлектрических и ферромагнитных веществ, можно описать с помощью векторных уравнений Максвелла в дифференциальной форме:
Или в скалярном виде:
Рассмотрим плоскую электромагнитную волну, покажем, что она является поперечной, и $\overrightarrow{E}\bot \ \overrightarrow{H}$. Допустим, что волна распространяется вдоль положительного направления $оси X$. В таком случае имеем:
Из первых уравнений систем (6) и (7) и уравнений (8) и (9) следует, что:
Из системы уравнений (12) можно сделать вывод о том, что $E_x\ и\ H_x$ не зависят ни от координат, ни от времени. Подобное стационарное и однородное поле не имеет отношения к электромагнитным волнам, поле которых нестационарное и неоднородное. Так, для поля плоской волны, которая распространяется вдоль $оси X$, имеем:
Колебания векторов $\overrightarrow{E}$ и $\overrightarrow{H}$ в точках плоскости $x=const$ отстают по времени от колебаний этих же векторов в точках плоскости $x=0$ на величину, равную $\frac{x}{v}$, где $v$ - скорость волны. Значит, $\overrightarrow{E}$ и $\overrightarrow{H}$ зависят от комбинации времени $(t)$ и отношения $\frac{x}{v}$ вида ($t-\frac{x}{v}$):
Введем обозначение вида: $\xi =t-\frac{x}{v},$ тогда получим выражения:
Подставим производные из (16) и (17) во второе и третье равнения систем выражений (6) и (7), получим:
Если учесть, что:
то уравнения (18) можно переписать в виде:
Интегрируя выражения (20) по $\xi $, положив постоянные интегрирования равными нулю, так как векторы $\overrightarrow{E}$ и $\overrightarrow{H}$ и их проекции на оси координат для переменного поля плоской волны не могут иметь постоянных составляющих, которые не зависят от $\xi =t-\frac{x}{v}$, в результате имеем:
Если скалярное произведение векторов будет равно нулю, при этом ни один из этих векторов не равен нулю, значит, эти векторы перпендикулярны. Найдем $\overrightarrow{E}\cdot \overrightarrow{H}$, используя выражение (21):
Из (22) очевидно, что $\overrightarrow{E}\bot \overrightarrow{H}$.
Взаимно перпендикулярные векторы $\overrightarrow{E}и\overrightarrow{H}$ колеблются в одной фазе, они одновременно становятся равными нулю и достигают максимума. Для любой бегущей волны, имеющей любую форму волновой поверхности, выполняется равенство:
Задание: Покажите, что векторы $\overrightarrow{v},\ \overrightarrow{E,\ \ }\overrightarrow{H}$ образуют правую тройку взаимно перпендикулярных векторов.
Решение:
Рассмотрим плоскую электромагнитную волну. Для нее если $\overrightarrow{E}=E_y\overrightarrow{j}$, то $\overrightarrow{H}=H_z\overrightarrow{k}$, причем если $E_y>0$, то и
\[H_z=\sqrt{\frac{\varepsilon {\varepsilon }_0}{\mu {\mu }_0}}E_y>0.\]Это доказывает, что $\overrightarrow{v},\ \overrightarrow{E,\ \ }\overrightarrow{H}$ - правая тройка взаимно перпендикулярных векторов.
Задание: Покажите на примере плоской электромагнитной волны, что векторы $\overrightarrow{E,\ \ }\overrightarrow{H}\ $совершают колебания в одной фазе.
Решение:
Из дифференциальных уравнений Максвелла следует, что для плоской электромагнитной волны, которая распространяется вдоль положительного направления $оси X$, выполняются равенства:
\[E_x=H_x=0\ (2.1),\] \[E_y=f_1\left(t-\frac{x}{v}\right),E_z=f_2\left(t-\frac{x}{v}\right)(2.2)\ ,\] \[H_y={\varphi }_1\left(t-\frac{x}{v}\right),H_z={\varphi }_2\left(t-\frac{x}{v}\right)(2.3).\] \[f_1=\sqrt{\frac{\mu {\mu }_0}{\varepsilon {\varepsilon }_0}}{\varphi }_2,\ f_2=-\sqrt{\frac{\mu {\mu }_0}{\varepsilon {\varepsilon }_0}}{\varphi }_1(2.4),\]следовательно, можно записать, что:
\[H_y=-\sqrt{\frac{\varepsilon {\varepsilon }_0}{\mu {\mu }_0}}\ E_z,\ H_z=-\sqrt{\frac{\varepsilon {\varepsilon }_0}{\mu {\mu }_0}}\ E_y\left(2.5\right).\]Зная, что:
\[H=\sqrt{{H_y}^2+{H_z}^2}и\ E=\sqrt{{E_y}^2+{E_z}^2}\left(2.6\right).\]Получим:
\[\sqrt{\mu {\mu }_0}H=\sqrt{\varepsilon {\varepsilon }_0}E.\]Что означает, что векторы напряженности электрического и магнитного полей совершают колебания в одной фазе.











