Что такое реальный газ
Реальным газом называют газ, между молекулами которого существуют заметные силы взаимодействия. В неидеальных, газах под высоким давлением, газах с большой плотностью взаимодействие молекул велико и его необходимо учитывать. Силы притяжения играют наиболее существенную роль на больших расстояниях между молекулами. Расстояние уменьшается, силы притяжения растут, но до определенного предела, затем они начинают уменьшаться и переходят в силы отталкивания. Притяжение и отталкивание молекул можно разделить и рассматривать и учитывать отдельно друг от друга.
Уравнение Ван-дер-Ваальса
Уравнение Ван-дер-Ваальса, описывающее состояние 1 моля реального газа, имеет вид:
где${\ V}_{\mu }$- молярный объем газа, $\frac{a}{V^2_{\mu }}$- внутреннее давление, обусловленное силами притяжения между молекулами, b -- поправка на собственный объем молекул, которая учитывает действие сил отталкивания между молекулами, причем
\[b=N_A\frac{2}{3}\pi d^3(2),\]где d- диаметр молекулы,
величина a вычисляется по формуле:
\[a=-2\pi N^2_A\int\nolimits^{\infty }_d{W_p\left(r\right)r^2dr\ \left(3\right),}\]где $W_p\left(r\right)$- потенциальная энергия притяжения двух молекул. Необходимо заметить, что газовая постоянная имеет индивидуальное значение для каждого вещества. Она отличается от молярной газовой постоянной, причем она меньше, что говорит об объединении молекул вещества в комплексы около критического состояния. Вдали от критических состояний можно использовать универсальную газовую постоянную.
С увеличением объема роль поправок в уравнении (1) становится менее существенной. И в пределе уравнение (1) переходит в уравнение состояния идеального газа для 1 моля (4):
\[pV=RT\ (4)\]Уравнение (4) -- уравнение Менделеева -- Клайперона, где m- масса газа, $R=8,31\ \frac{Дж}{моль\cdot К}$- универсальная газовая постоянная.
Это согласуется с тем фактом, что при уменьшении плотности реальные газы по своим свойствам приближаются к идеальным.
Уравнение (1) может быть записано в вириальной форме:
\[{pV}_m=RT+\frac{RTb'-a'}{V_m}+RT\sum\limits^{\infty }_{n=2}{\frac{{b'}^n}{V^n_m}}\ \left(5\right),\]где $V_m=\frac{V}{\nu }.$
Для анализа изотерм уравнение (1) удобнее представить в виде:
\[V^3_m-\left(b'+\frac{RT}{p}\right)V^2_m+\frac{a'V_m}{p}-\frac{a'b}{p}=0\left(6\right).\]Рассматриваемое уравнение может описывать и свойства жидкости, например плохую ее сжимаемость.
На рис.1 изображена изотерма Ван-дер-Ваальса для некоторого постоянного значения температуры T, построенная из соответствующего уравнения.
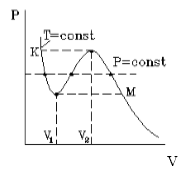
Рис.1
Такая зависимость на практике невозможна. Опыт показывает, что график должен иметь вид рис.2 то есть существуют области, в которых при изменении объема давление неизменно. В некоторых отрезках график изотермы параллелен оси V (рис 2). Это область фазового перехода. Жидкость и газ существую одновременно.
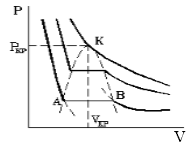
Рис.2
По мере увеличения температуры участок, отражающий состояние нахождения газа одновременно в двух фазах на графиках p(V), сужается и превращается в точку (рис. 2). Это особая точка К, в которой пропадает различие между жидкостью и паром. Это так называемая критическая точка.
Итак, уравнение Ван-дер-Ваальса описывает поведение газов близких к реальным. Их можно применить к газообразной и жидкой фазам вещества. Эти уравнения отражают существование фазового перехода газ -- жидкость. Показывают наличие критической точки перехода. Однако абсолютно точных количественных результатов расчеты, в которых используются вышеназванные уравнения, не дают.
Задание: Газ в количестве 1 моль находится в сосуде объемом V л при температуре $T_1$ давление газа $p_1$, а при $T_2$ давление газа $p_2$. Найти постоянные Ван-дер-Ваальса.
Решение:
Запишем уравнение Ван-дер-Ваальса для одного моля реального газа для состояний 1 и 2:
\[\left(p_1+\frac{a}{V^2_{\mu }}\right)\left(V_{\mu }-b\right)=RT_1\ \left(1.1\right).\] \[\left(p_2+\frac{a}{V^2_{\mu }}\right)\left(V_{\mu }-b\right)=RT_2\ \left(1.2\right).\]Раскроем скобки в (1.1):
\[p_1V_{\mu }+\frac{a}{V_{\mu }}-p_1b-\frac{ab}{V^2_{\mu }}=RT_1\ \left(1.3\right).\] \[p_2V_{\mu }+\frac{a}{V_{\mu }}-p_2b-\frac{ab}{V^2_{\mu }}=RT_2\left(1.4\right).\]Вычтем $\left(1.4\right).\ из\ \left(1.3\right):$
\[p_1V_{\mu }+\frac{a}{V_{\mu }}-p_1b-\frac{ab}{V^2_{\mu }}-p_2V_{\mu }-\frac{a}{V_{\mu }}+p_2b+\frac{ab}{V^2_{\mu }}=RT_1-RT_2\to \] \[p_1V_{\mu }-p_1b-p_2V_{\mu }{+p}_2b=RT_1-RT_2\] \[-p_1b{+p}_2b=RT_1-RT_2-p_1V_{\mu }+p_2V_{\mu }\to b=\frac{RT_1-RT_2-p_1V_{\mu }+p_2V_{\mu }}{p_2-p_1}\left(1.5\right).\]Выразим a из (1.1):
\[a\left(\frac{1}{V_{\mu }}-\frac{b}{V^2_{\mu }}\right)=RT_1-p_1V_{\mu }+p_1b\to a=\frac{RT_1-p_1V_{\mu }+p_1b}{\left(\frac{1}{V_{\mu }}-\frac{b}{V^2_{\mu }}\right)}\]Ответ: $b=\frac{RT_1-RT_2-p_1V_{\mu }+p_2V_{\mu }}{p_2-p_1},\ a=\frac{RT_1-p_1V_{\mu }+p_1b}{\left(\frac{1}{V_{\mu }}-\frac{b}{V^2_{\mu }}\right)}$.
Задание: Для реального газа, используя уравнение Ван-дер-Ваальса, получите уравнение адиабаты в параметрах V и T.
Решение:
Запишем первое начало термодинамики:
\[\delta Q=dU+\partial A=0\ \left(\ 2.1\right)\]Так как процесс адиабатный, то он идет теплообмена. Перепишем уравнение (2.1) для ван-дер-ваальсовского газа, зная, что:
\[dU=\frac{i}{2}\nu RdT-\frac{a}{V+dV}+\frac{a}{V}=\frac{i}{2}\nu RdT+\frac{adV}{V^2}\ (2.2)\]получим:
\[0=pdV+\frac{i}{2}\nu RdT+\frac{adV}{V^2}\ (2.3)\] \[0=(p+\frac{a}{V^2})dV+\frac{i}{2}\nu RdT\ (2.4)\]Из уравнения Ван-дер-Ваальса:
\[\left(p+\frac{a}{V^2}\right)\left(V-b\right)=RT\ \to p+\frac{a}{V^2}=\frac{RT}{\left(V-b\right)}\ \left(2.5\right)\]Подставим (2.5) в (2.4), разделим переменные:
\[\frac{RT}{\left(V-b\right)}dV+\frac{i}{2}\nu RdT\ =0\to \frac{Rd(V-b)}{\left(V-b\right)}=-\frac{i}{2}\nu R\frac{dT}{T}(2.6)\ \] \[\frac{d(V-b)}{\frac{i}{2}\nu \left(V-b\right)}=-\frac{dT}{T}(2.7)\ \]Проинтегрируем (2.7):
ln$\left({\left(V-b\right)}^{\frac{i}{2}\nu }T\right)=0\to {\left(V-b\right)}^{\frac{i}{2}\nu }T=const.$Ответ: Уравнение адиабаты для заданного случая имеет вид: ${\left(V-b\right)}^{\frac{i}{2}\nu }T=const.$












