Симметрия волновой функции относительно перестановки электронов

Пусть система, содержит две одинаковые частицы. В стационарном состоянии волновая функция от времени не зависит, представим ее как: $\psi (q_1,\ q_2)$. При этом если не учитываются спины частиц $q_1$ - три пространственные координаты одной частицы, $q_2$ - координаты второй частицы. (Если требуется учесть спин, то к пространственным координатам добавляют спиновые координаты).

При перестановке местами частиц $1$ и $2$, получится волновая функция $\psi \left(q_2,\ q_1\right).$ Такая операция может быть представлена, как воздействие линейного оператора $\hat{P}$ на функцию $\psi (q_1,\ q_2)$. Такой оператор называется оператором перестановки:

Проведем перестановку еще раз, получим:

Из выражения (2) следует, что ${\hat{P}}^2=1$, значит $\hat{P}=\pm 1.\ $Значит, допустимыми являются волновые функции видов:

Если волновая функция неизменна (3) при перестановке частиц, ее называют симметричной (это обозначено индексом $s$). Выражение (4) дает нам определение ассиметричной функции, такая функция у нас имеет индекс $a$. Она меняет знак в случае перестановки одинаковых частиц.

Данные результаты обобщаются для систем имеющих любое количество одинаковых частиц. Тогда симметрия или асимметрия проявляется при перестановке любых двух частиц.

Сделаем обобщение для системы из $N$ частиц. $\psi$ -функция для системы из $N$ частиц:

Электроны являются фермионами, следовательно, их состояния описываются при помощи антисимметричных волновых функций. В выражении (5) обозначаем совокупность всех координат и всех спиновых переменных как $q_i$ данных $N$ электронов.

Если рассмотреть систему невзаимодействующих фермионов, то антисимметричная волновая функция систему, состоящую из $N$ частиц, можно описать в виде:

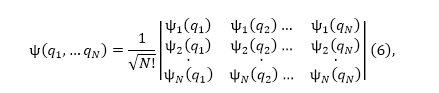
Рисунок 1.

где $\psi_i\left(q_i\right)$ -- волновые функции, описывающие поведение одной частицы. Волновая функция для множества частиц, записанная в виде (6) названа детерминантом Слэтера. При использовании детерминантной записи перестановки частиц то же самое, что перестановки двух столбцов в определителе (6). Мы помним, что перестановка столбцов изменит знак детерминанта, что будет соответствовать тому, что волновая функция является антисимметричной.

Если одинаковые электроны не взаимодействуют, то можно рассматривать не только состояние системы в целом, но и говорить о состоянии одной частицы. Так, говорят: одна частица пребывает в состоянии $\psi_a,\ $а другая - в $\psi_b$. В системе одинаковых фермионов, к которым относятся электроны, не может быть двух частиц, которые находились бы в одном и том же состоянии. Данный постулат называют принципом или запретом Паули.

В смысле ясности и точности принцип Паули проигрывает принципу антисимметрии волновых функций. Принцип Паули сформулирован для состояний отдельных частиц, тогда как принцип антисимметрии выполняется при наличии взаимодействия частиц. Принцип антисимметрии волновых функций фермионов иногда называют обобщенным принципом Паули.

Сформулируем требование: Система из $N$ электронов должна иметь определенный суммарный спин. Вспомним, что для одного электрона любой оператор, который действует на спиновую переменную можно представить как линейную комбинацию трех операторов: ${\sigma }_x,{\sigma }_y,{\sigma }_z$. При этом выполняются равенства:

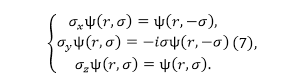
Рисунок 2.

где $r$ -- система $3$ пространственных координат, $\sigma $ -- спиновая переменная, принимающая два значения (например, $\sigma =1$ и $\sigma =-1$). Рассматривая волновую функцию как состоящую из двух компонент ($\psi \left(r,1\right)\ и\ \psi \left(r,-1\right)$) можно записать:

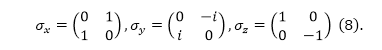
Рисунок 3.

При этом операторы:

будут удовлетворять перестановочным соотношениям:

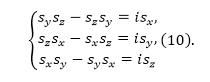
Рисунок 4.

Перестановочные соотношения (10) определяют свойства момента количества движения (в единицах $\hbar $). Их можно считать операторами компонент собственного момента количества движения электрона. Если электронов много, то операторы ${\sigma }_{lx},{\sigma }_{ly},{\sigma }_{lz}$, действующие на спиновую переменную электрона с номером $l$ можно записать как:

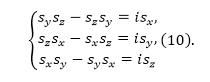
Рисунок 5.

Операторы компонент спинового момента количества движения совокупности электронов (в единицах $\hbar $) выразим как:

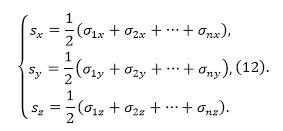
Рисунок 6.

Данные операторы удовлетворяют перестановочным соотношениям (10). Из них следует, что оператор:

будет коммутировать с каждым из операторов $s_x$, $s_y,\ s_z$. Собственные значения этого оператора равны $s(s+1)$, где $s$ -- равна половине целого неотрицательного числа. При известном $s$, собственные значения каждого из операторов $s_x$, $s_y,\ s_z$ изменяются как:

Требование, чтобы система из $N$ электронов имела определённый результирующий спин, можем записать как: